Leaky Cauldron

打印字符串的子序列

Posted on 2020-06-28 Edited on 2022-07-20

题目

打印一个字符串的全部子序列, 包括空字符串

题解

迭代过程中, 要么当前字符保留, 要么略过

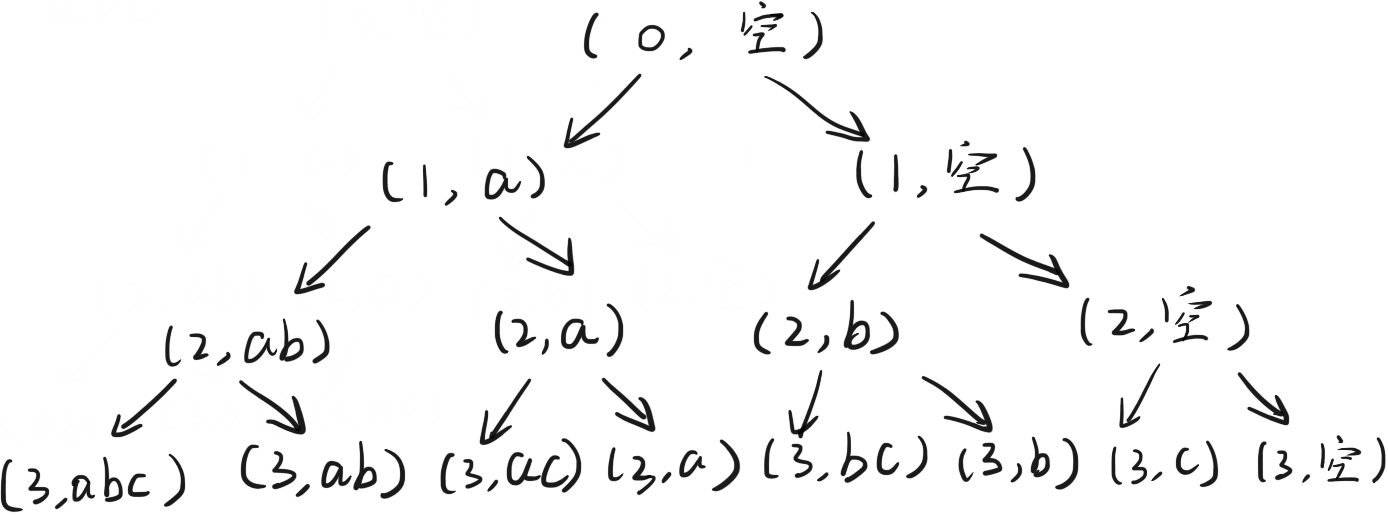
Java

public class Subsequence {
    public static void printAllSub(String str) {
        char[] chs = str.toCharArray();
        process(chs, 0, "");
        System.out.println("");
    }

    public static void process(char[] chs, int i, String pre) {
        if (i == chs.length) {
            if (!pre.equals("")) {
                System.out.println(pre);
            }
            return;
        }
        process(chs, i + 1, pre + String.valueOf(chs[i]));
        process(chs, i + 1, pre);
    }

    public static void main(String[] args) {
        String test = "abc";
        printAllSub(test);
    }
}

abc
ab
ac
a
bc
b
c

Python

def print_subsequence(string):
    str_arr = [i for i in string]
    process(str_arr, 0, '')
    print()


def process(str_arr, i, pre):
    if i == len(str_arr):
        if pre != '':
            print(pre)
        return
    process(str_arr, i + 1, pre + str_arr[i])
    process(str_arr, i + 1, pre)

汉诺塔问题

Posted on 2020-06-27 Edited on 2022-07-20

题目

打印 n 层汉诺塔从最左边移动到最右边的全部过程

题解

假定三根柱子分别为 from , to 和 help , 该问题可划分为 3 个步骤

将 1~(n-1) 从 from 移动到 help 上
将 n 从 from 移动到 to 上
将 1~(n-1) 从 help 移动到 to 上

其中, 将 1~(n-1) 从 help 移动到 to 的过程又可分为多个子问题, 需不断调整三个柱子的角色.

Java

public class Hannoi {
    public static void hannoi(int n, String from, String to, String help) {
        if (n == 1) {
            System.out.println("move " + 1 + " from " + from + " to " + to);
        } else {
            hannoi(n - 1, from, help, to);
            System.out.println("move " + n + " from " + from + " to " + to);
            hannoi(n - 1, help, to, from);
        }
    }

    public static void main(String[] args) {
        int n = 3;
        hannoi(3, "left", "right", "mid");
    }
}

Python

def hannoi(n, source, target, assist):
    if n == 1:
        print('move 1 from ' + source + ' to ' + target)
    else:
        hannoi(n - 1, source, assist, target)
        print('move ' + str(n) + ' from ' + source + ' to ' + target)
        hannoi(n - 1, assist, target, source)

限重最大值问题

Posted on 2020-06-26 Edited on 2022-07-20

题目

给定两个数组 w 和 v ，两个数组长度相等，w[i] 表示第i件商品的重量，v[i] 表示第i件商品的价值。再给定一个整数 bag ，要求你挑选商品的重量加起来一定不能超过 bag ，返回满足这个条件下，你能获得的最大价值。

题解

解法类似上一篇博客

暴力递归

穷举所有可能的结果, 迭代过程中判断累计重量 acc_weight 是否超过 bag , 若超过则返回 Integer.MIN_VALUE , 相当于直接舍弃该分支. 另一个迭代的基础条件为当 i 达到 w.length 时, 返回 0 , 因为第 i 次递归的返回值为当前商品的价值 v[i] 加上后续商品的价值与只有后续商品价值二者中的较大者, i 等于 w.length 时, 没有后续商品, 故直接返回 0 .

Java

public class Knapsack {
    public static int maxValue(int[] w, int[] v, int i, int accWeight, int bag) {
        if (accWeight > bag) {
            return Integer.MIN_VALUE;   // 重量超过 bag, 舍弃
        }

        if (i == w.length) {
            return 0;
        }

        return Math.max(
                maxValue(w, v, i + 1, accWeight, bag),
                v[i] + maxValue(w, v, i + 1, accWeight + w[i], bag)
        );
    }

    public static void main(String[] args) {
        int[] w = {3, 2, 4, 7};
        int[] v = {5, 6, 3, 19};
        int bag = 11;

        System.out.println(maxValue(w, v, 0, 0, bag));
    }
}

Python

def max_value(w, v, i, acc_weight, bag):
    if acc_weight > bag: return float('-inf')

    if i == len(w): return 0

    return max(
        max_value(w, v, i + 1, acc_weight, bag),
        v[i] + max_value(w, v, i + 1, acc_weight + w[i], bag)
    )

动态规划

此类无后效性的递归问题均可转化为动态递归.

步骤

分析可变参数, 求出表空间
确定最终状态
根据 base case 确定初始状态
分析一个普遍位置的依赖关系
根据依赖顺序, 逆序求出整张表

Java

public class Knapsack {
    public static int maxValue(int[] w, int[] v, int bag) {
        int[][] dp = new int[w.length + 1][bag + 1];

        for (int i = 0; i <= bag; i++) {
            dp[w.length][i] = 0;
        }

        for (int i = w.length - 1; i >= 0; i--) {
            for (int j = bag; j >= 0; j--) {
                dp[i][j] = dp[i + 1][j];
                if (j + w[i] <= bag)
                    dp[i][j] = Math.max(
                            dp[i + 1][j],
                            dp[i + 1][j + w[i]] + v[i]
                    );
            }
        }

        return dp[0][0];
    }
}

Python

def max_value(w, v, bag):
    dp = [[0] * (bag + 1) for _ in range(len(w) + 1)]

    for i in range(len(w) - 1, -1, -1):
        for j in range(bag, -1, -1):
            dp[i][j] = dp[i + 1][j]
            if j + w[i] <= bag:
                dp[i][j] = max(
                    dp[i + 1][j],
                    dp[i + 1][j + w[i]] + v[i]
                )
                
    return dp[0][0]

数组累加得到目标值

Posted on 2020-06-24 Edited on 2022-07-20

题目

给定一个正整数数组 arr 和一个整数 target , 如果可以任意选择 arr 中的数字, 求能否累加得到 target .

题解

暴力解法

穷举所有可能的和, 判断是否含有 target , 穷举过程如下, 其中中间变量格式为 (i, sum) , i 为索引, sum 为当前的累加和, 左支表示累加 arr[i] , 右支表示跳过该值.

Java

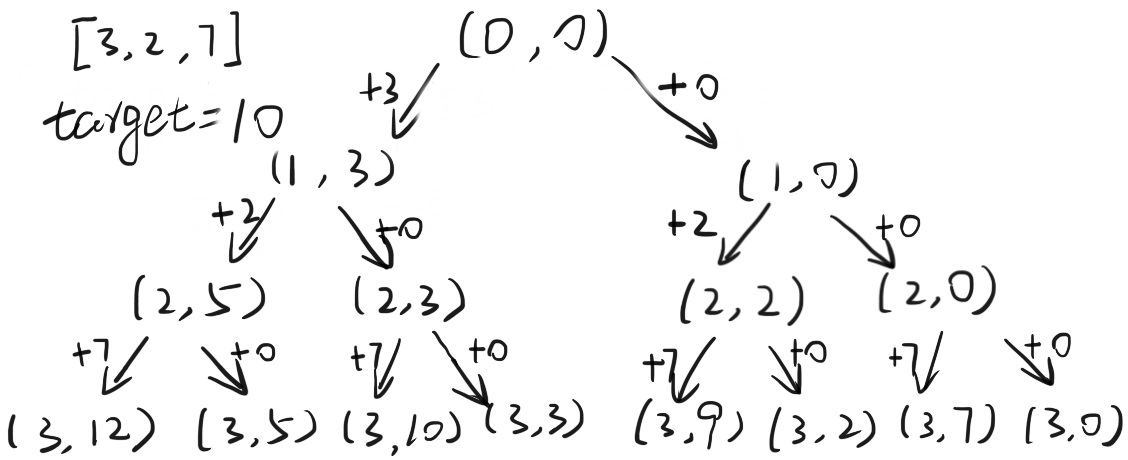
public class SumToTarget {
    public static boolean isSum(int[] arr, int i, int sum, int target) {
        if (i == arr.length)
            return sum == target;

        // 左分支 || 右分支
        return isSum(arr, i + 1, sum + arr[i], target) || isSum(arr, i + 1, sum, target);
    }

    public static void main(String[] args) {
        int[] arr = {3, 2, 7};
        int target = 10;
        System.out.println(isSum(arr, 0, 0, target));
    }
}

Python

def sum_to_target(arr, i, cur_sum, target):
    if i == len(arr):
        return cur_sum == target

    return sum_to_target(arr, i + 1, cur_sum + arr[i], target) or \
		   sum_to_target(arr, i + 1, cur_sum, target)


if __name__ == '__main__':
    arr = [2, 3, 7]
    target = 10
    print(sum_to_target(arr, 0, 0, target))

动态规划

将暴力递归改进为动态规划时, 无需考虑原题目的含义, 只需找到迭代时各变量之间的依赖关系即可. 递归到动态规划的转化方法:

递归函数有 n 个参数, 就定义一个 n 维的数组
数组的下标是递归函数参数的取值范围
数组元素的值是递归函数的返回值, 这样就可以从边界值开始，逐步填充数组，相当于计算递归函数值的逆过程。

1	return isSum(arr, i + 1, sum + arr[i], target) \|\| isSum(arr, i + 1, sum, target);

由上述代码知递归函数第 i 次递归的结果只依赖于 i+1 和 sum , 故需定义一个 i+1 和 sum 状态关系的数组. 递归函数参数 i 的取值范围为 0~arr.length , sum 的范围为全部元素都不取到全部元素的和, 以 [3, 2, 7] 为例即为 0~12 . 构成的数组如下:

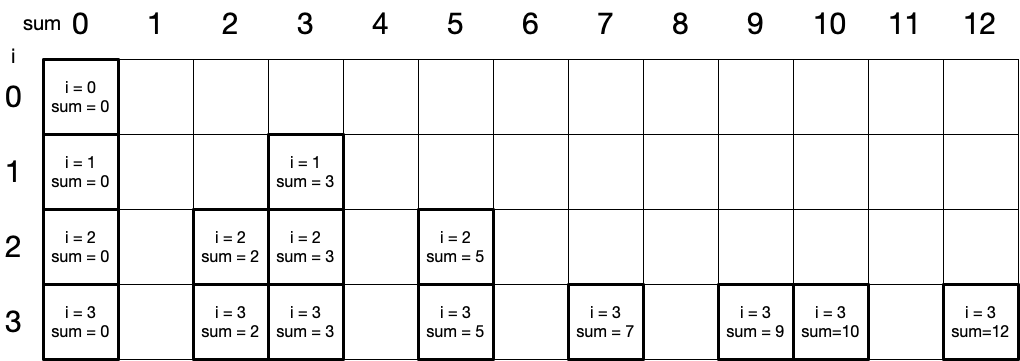
任意一格 (i, sum) 的值仅由 (i+1, sum) 和 (i+1, sum+arr[i]) 决定. 如上表所示, (1, 3) 的值取决于 (1+1, 3) 和 (1+1, 3+arr[1]) , 其中 arr[1] 为 2, 故 (1, 3) 的真值取决于 (2, 3) 和 (2, 5) 的真值.

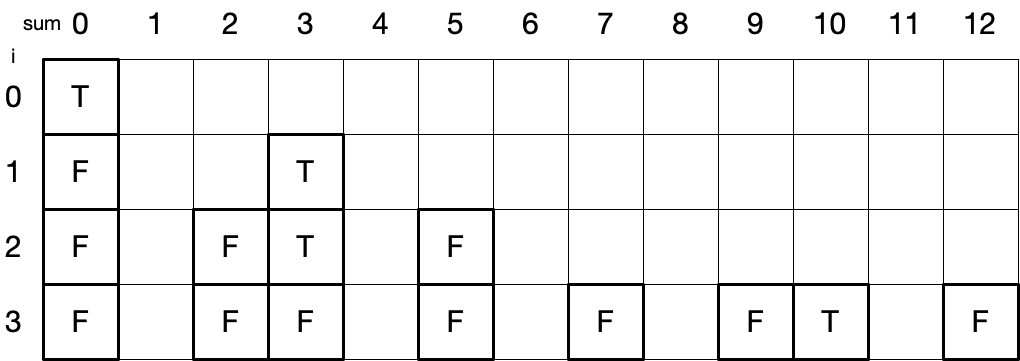
最终结果返回表中 (0, 0) 位置即可.

Java

public class SumToTarget {
    public static boolean isSum(int[] arr, int target) {
        // 本题只要有一列达到 target 即可, 故 target + 1 列即可
        boolean[][] dp = new boolean[arr.length + 1][target + 1];
        // target 列必为 True
        dp[i][target] = true;

        for (int i = arr.length - 1; i >= 0; i--) {
            for (int j = target; j >= 0; j--) {
                dp[i][j] = dp[i + 1][j];
                if (j + arr[i] <= target) {
                    dp[i][j] = dp[i][j] || dp[i + 1][j + arr[i]];
                }
            }
        }
        return dp[0][0];
    }
}

Python

def sum_to_target(arr, target):
    row = len(arr)
    dp = [[False] * (target + 1) for _ in range(row + 1)]

    dp[row][target] = True

    for i in range(row - 1, -1, -1):
        for j in range(target, -1, -1):
            if j + arr[i] <= target:
                dp[i][j] = dp[i + 1][j] or dp[i + 1][j + arr[i]]
            else:
                dp[i][j] = dp[i + 1][j]

    return dp[0][0]

二维数组最小路径和

Posted on 2020-06-24 Edited on 2022-07-20

题目 (LeetCode #64)

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明: 每次只能向下或者向右移动一步。

示例:

输入:

[
    [1, 3, 1],
    [1, 5, 1],
    [4, 2, 1]
]

输出: 7

题解

暴力递归

从左上角到右下角, 每次移动只有向右或向下两种可能, 需递归地找出左右两个方向到右下角路径和较小者即可.

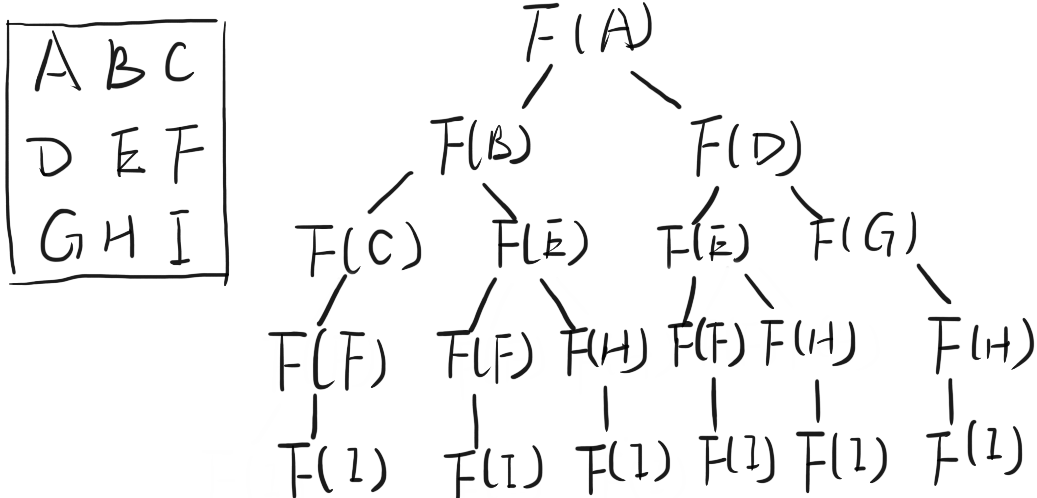
暴力递归不记录子状态的结果, F(E) , F(H), F(F) 进行了多次重复计算, 占用较多空间, 数据较多时会超时, 可改用计划搜索的方法进行优化.

Java

public class MinimalPathSum {
	public int minPathSum(int[][] grid) {
        if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
            return 0;
        }
        return process(grid, 0, 0);
    }

    public static int process(int[][] grid, int i, int j) {
        if (i == grid.length - 1 && j == grid[0].length - 1)
            return grid[i][j];

        if (i == grid.length - 1)
            return grid[i][j] + process(grid, i, j + 1);

        if (j == grid[0].length - 1)
            return grid[i][j] + process(grid, i + 1, j);

        return grid[i][j] + Math.min(process(grid, i, j + 1), process(grid, i + 1, j));
    }
}

Python

def get_minimal_path_sum(grid):
    if not grid or len(grid) < 1 or not grid[0] or len(grid[0]) < 1:
        return 0
    return process(grid, 0, 0)


def process(grid, i, j):
    if i == len(grid) - 1 and j == len(grid[0]) - 1:
        return grid[i][j]

    if i == len(grid) - 1:
        return grid[i][j] + process(grid, i, j + 1)
    if j == len(grid[0]) - 1:
        return grid[i][j] + process(grid, i + 1, j)

    return grid[i][j] + min(process(grid, i + 1, j), process(grid, i, j + 1))

计划搜索

将每个子状态的运算结果存入缓存中, 若之前计算过则直接返回计算结果.

Java

public class MinimalPathSum {
    static HashMap<String, Integer> cache;

    public static int minimalPathSum(int[][] grid) {
        if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
            return 0;
        }

        cache = new HashMap<>();
        return process(grid, 0, 0);
    }

    public static int process(int[][] grid, int i, int j) {
        String key = i + "_" + j;
        if (cache.containsKey(key)) {
            return cache.get(key);	// 存入 Map 时, 已经包含了 grid[i][j] 的值, 故不需重复加
        }

        int result = 0;
        if (i == grid.length - 1 && j == grid[0].length - 1) {
            result = grid[i][j];
        } else if (i == grid.length - 1) {
            result = grid[i][j] + process(grid, i, j + 1);
        } else if (j == grid[0].length - 1) {
            result = grid[i][j] + process(grid, i + 1, j);
        } else {
            result = grid[i][j] + Math.min(process(grid, i + 1, j), process(grid, i, j + 1));
        }

        cache.put(key, result);
        return result;
    }
}

Python

class MinimalPathSum:
    def __init__(self):
        self.result_dict = None

    def get_minimal_path_sum(self, grid):
        if not grid or len(grid) < 1 or not grid[0] or len(grid[0]) < 1:
            return 0

        self.result_dict = dict()
        return self.process(grid, 0, 0)

    def process(self, grid, i, j):
        key = str(i) + "_" + str(j)
        if self.result_dict.get(key):
            return self.result_dict.get(key)

        if i == len(grid) - 1 and j == len(grid[0]) - 1:
            result = grid[i][j]
        elif i == len(grid) - 1:
            result = grid[i][j] + self.process(grid, i, j + 1)
        elif j == len(grid[0]) - 1:
            result = grid[i][j] + self.process(grid, i + 1, j)
        else:
            result = grid[i][j] + min(self.process(grid, i + 1, j), self.process(grid, i, j + 1))

        self.result_dict[key] = result
        return result

动态规划

左上角到右下角的最短距离与右下角到左上角最短距离相同, 为便于表示, 以下改为求右下角到左上角的最短距离.

由以上计划搜索部分知, 当矩阵中某点的位置即 i 和 j 的值确定时, 该点到左上角的最短路径就确定了, 故可单独求出矩阵中各元素到左上角的最短路径, 每个元素的最短路径值仅由其相邻的左边和上边元素决定, 其对应关系如下例, 故输出矩阵中的右下角即为左上角到右下角的最短距离.

输入

3	8	6	0	5	9	9	6	3	4	0	5	7	3	9	3	
0	9	2	5	5	4	9	1	4	6	9	5	6	7	3	2	
8	2	2	3	3	3	1	6	9	1	1	6	6	2	1	9	
1	3	6	9	9	5	0	3	4	9	1	0	9	6	2	7	
8	6	2	2	1	3	0	0	7	2	7	5	4	8	4	8	
4	1	9	5	8	9	9	2	0	2	5	1	8	7	0	9	
6	2	1	7	8	1	8	5	5	7	0	2	5	7	2	1	
8	1	7	6	2	8	1	2	2	6	4	0	5	4	1	3	
9	2	1	7	6	1	4	3	8	6	5	5	3	9	7	3	
0	6	0	2	4	3	7	6	1	3	8	6	9	0	0	8	
4	3	7	2	4	3	6	4	0	3	9	5	3	6	9	3	
2	1	8	8	4	5	6	5	8	7	3	7	7	5	8	3	
0	7	6	6	1	2	0	3	5	0	8	0	8	7	4	3	
0	4	3	4	9	0	1	9	7	7	8	6	4	6	9	5	
6	5	1	9	9	2	2	7	4	2	7	2	2	3	7	2	
7	1	9	6	1	2	7	0	9	6	6	4	4	5	1	0	
3	4	9	2	8	3	1	2	6	9	7	0	2	4	2	0	
5	1	8	8	4	6	8	5	2	4	1	6	2	2	9	7

输出

3	11	17	17	22	31	40	46	49	53	53	58	65	68	77	80	
3	12	14	19	24	28	37	38	42	48	57	62	68	75	78	80	
11	13	15	18	21	24	25	31	40	41	42	48	54	56	57	66	
12	15	21	27	30	29	25	28	32	41	42	42	51	57	59	66	
20	21	23	25	26	29	25	25	32	34	41	46	50	58	62	70	
24	22	31	30	34	38	34	27	27	29	34	35	43	50	50	59	
30	24	25	32	40	39	42	32	32	36	34	36	41	48	50	51	
38	25	32	38	40	47	43	34	34	40	38	36	41	45	46	49	
47	27	28	35	41	42	46	37	42	46	43	41	44	53	53	52	
47	33	28	30	34	37	44	43	43	46	51	47	53	53	53	60	
51	36	35	32	36	39	45	47	43	46	55	52	55	59	62	63	
53	37	43	40	40	44	50	52	51	53	56	59	62	64	70	66	
53	44	49	46	41	43	43	46	51	51	59	59	67	71	74	69	
53	48	51	50	50	43	44	53	58	58	66	65	69	75	83	74	
59	53	52	59	59	45	46	53	57	59	66	67	69	72	79	76	
66	54	61	65	60	47	53	53	62	65	71	71	73	77	78	76	
69	58	67	67	68	50	51	53	59	68	75	71	73	77	79	76	
74	59	67	75	72	56	59	58	60	64	65	71	73	75	84	83

Java

public class MinimalPathSum {
	public static int dynamicProgramming(int[][] grid) {
        if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
            return 0;
        }

        int row = grid.length;
        int column = grid[0].length;

        int[][] dp = new int[row][column];

        dp[0][0] = grid[0][0];

        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }

        for (int j = 1; j < column; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }

        for (int i = 1; i < row; i++) {
            for (int j = 1; j < column; j++) {
                dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
            }
        }

        for (int i = 0; i < row; i++) {
            for (int j = 0; j < column; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println();
        }

        return dp[row - 1][column - 1];
    }
}

Python

class MinimalPathSum:
    def dynamic_programming(grid):
        if not grid or len(grid) < 1 or not grid[0] or len(grid[0]) < 1: return 0

        row = len(grid)
        column = len(grid[0])

        dp = [[0] * column for _ in range(row)]

        dp[0][0] = grid[0][0]

        for i in range(1, row):
            dp[i][0] = grid[i][0] + dp[i - 1][0]

        for j in range(1, column):
            dp[0][j] = grid[0][j] + dp[0][j - 1]

        for i in range(1, row):
            for j in range(1, column):
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]

        return dp[row - 1][column - 1]

最小生成树

Posted on 2020-06-22 Edited on 2022-07-20

最小生成树是一副连通加权无向图中一棵权值最小的生成树。一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和 (Wikipedia)。

常见算法有 Kruskal 算法和 Prim 算法

Kruskal 算法

按照边的权重顺序（从小到大）将边加入生成树中，但是若加入该边会与生成树形成环则不加入该边。直到树中含有顶点数减一条边为止。这些边组成的就是该图的最小生成树。

实现过程中, 可利用小根堆来依次返回权重最小的边, 利用并查集来避免生成树形成回路.

Java

UnionFind 定义如下

class UnionFind {
    public HashMap<GraphNode, GraphNode> parentMap;
    public HashMap<GraphNode, Integer> sizeMap;

    public UnionFind(Collection<GraphNode> nodes) {
        parentMap = new HashMap<>();
        sizeMap = new HashMap<>();

        // 初始化并查集, 此时每个结点自成一个集合, 指针指向它本身
        for (GraphNode node : nodes) {
            parentMap.put(node, node);
            sizeMap.put(node, 1);
        }
    }

    /**
     * 找到代表结点并整理结点
     *
     * @param node 当前节点
     * @return 代表结点
     */
    private GraphNode findHead(GraphNode node) {
        GraphNode parent = parentMap.get(node);
        if (parent != node) {
            parent = findHead(parent);
        }

        parentMap.put(node, parent);    // 整理结点
        return parent;
    }

    public boolean isSameSet(GraphNode node1, GraphNode node2) {
        return findHead(node1) == findHead(node2);
    }

    public void union(GraphNode a, GraphNode b) {
        if (a == null || b == null)
            return;
        GraphNode aHead = findHead(a);
        GraphNode bHead = findHead(b);

        if (aHead == bHead)
            return;

        int aSetSize = sizeMap.get(aHead);
        int bSetSize = sizeMap.get(bHead);

        if (aSetSize <= bSetSize) {
            parentMap.put(aHead, bHead);
            sizeMap.put(bHead, aSetSize + bSetSize);
        } else {
            parentMap.put(bHead, aHead);
            sizeMap.put(aHead, aSetSize + bSetSize);
        }
    }
}

Kruskal 实现

public class KruskalMST {
    public static Set<Edge> kruskalMST(Graph graph) {
        UnionFind unionFind = new UnionFind(graph.nodes.values());
        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>((a, b)->{
            return a.weight - b.weight;
        });

        priorityQueue.addAll(graph.edges);

        Set<Edge> result = new HashSet<>();
        while (!priorityQueue.isEmpty()) {
            Edge edge = priorityQueue.poll();
            if (!unionFind.isSameSet(edge.from, edge.to)) {
                result.add(edge);
                unionFind.union(edge.from, edge.to);
            }
        }

        return result;
    }
}

Python

UnionFindSet 定义见并查集

由于 Edge 对象不能够直接比较大小, 需重写 Edge 的比较函数, __lt__ 对应 < , __gt__ 对应 > , 只重写其中一个, 另一个会自动取反. 比较相等时结果相同.

class Edge:
    def __init__(self, weight, from_node, to_node):
        self.weight = weight
        self.from_node = from_node
        self.to_node = to_node

    def __lt__(self, other):
        # 重写 < 比较函数
        return True if self.weight < other.weight else False

Kruskal 实现

from heapq import *

def kruskal_mst(graph):
    union_find_set = UnionFindSet(graph.nodes.values())
    heap = []

    for edge in graph.edges:
        heappush(heap, edge)

    result = set()

    while heap:
        edge = heappop(heap)
        if not union_find_set.is_same_set(edge.from_node, edge.to_node):
            result.add(edge)
            union_find_set.union(edge.from_node, edge.to_node)

    return result

Prim 算法

从任意一个节点开始, 将与其相连的几条边全部放入一个小根堆中, 每次弹出小根堆中权重最小的边, 获取该边的另一端节点放入集合中, 并将另一端节点的所有直接相连的边放入小根堆中, 迭代直到小根堆中的边全部取出为止.

Java

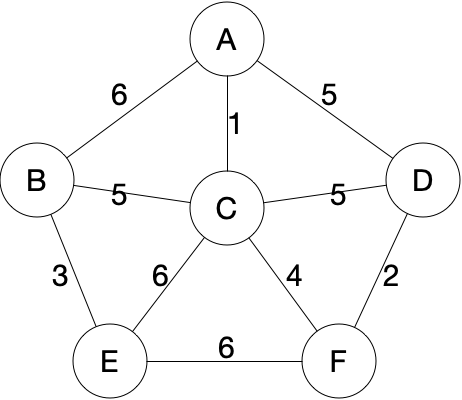
public class PrimMST {
    public static Set<Edge> primMST(Graph graph) {
        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>((a, b) -> {
            return a.weight - b.weight;
        });
        HashSet<GraphNode> set = new HashSet<>();
        Set<Edge> result = new HashSet<>();
		
        // 遍历所有节点, 考虑到可能有多棵生成树不相连的情况
        for (GraphNode node : graph.nodes.values()) {
            if (!set.contains(node)) {
                set.add(node);
                priorityQueue.addAll(node.edges);

                while (!priorityQueue.isEmpty()) {
                    Edge edge = priorityQueue.poll();
                    GraphNode toNode = edge.to;
                    if (!set.contains(toNode)) {
                        set.add(toNode);
                        result.add(edge);
                        priorityQueue.addAll(toNode.edges);
                    }
                }
            }
        }
        return result;
    }

    public static void main(String[] args) {
        // Prim 算法需沿着边迭代加入点, 故建立无向图时需建立双向指针
        Integer[][] nodes = {
                {6, 1, 2}, {6, 2, 1},
                {1, 1, 3}, {1, 3, 1},
                {5, 1, 4}, {5, 4, 1},
                {5, 2, 3}, {5, 3, 2},
                {3, 2, 5}, {3, 5, 2},
                {5, 3, 4}, {5, 4, 3},
                {4, 3, 6}, {4, 6, 3},
                {6, 3, 5}, {6, 5, 3},
                {2, 4, 6}, {2, 6, 4},
                {6, 5, 6}, {6, 6, 5}
        };
        Graph graph = Code_26_GraphBuilder.createGraph(nodes);
        Set<Edge> result = primMST(graph);
        for (Edge edge : result) {
            System.out.println(edge.weight);
        }
    }
}

1 3 2 4 5

Python

def prim_mst(graph):
    edge_heap = []
    node_set = set()
    result = set()

    for node in graph.nodes.values():
        if node not in node_set:
            node_set.add(node)
            for edge in node.edges:
                heappush(edge_heap, edge)

            while edge_heap:
                edge = heappop(edge_heap)
                to_node = edge.to_node
                if to_node not in node_set:
                    node_set.add(to_node)
                    result.add(edge)
                    for next_edge in to_node.edges:
                        heappush(edge_heap, next_edge)
    return result

拓扑排序算法

Posted on 2020-06-21 Edited on 2022-09-30

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，才能称为该图的一个拓扑排序（Topological sorting）：

序列中包含每个顶点，且每个顶点只出现一次；
若A在序列中排在B的前面，则在图中不存在从B到A的路径。

适用范围:

有向图
有入度为 0 的节点
图中没有环

拓扑排序常应用于有依赖关系的一组事务之间的排序. 例如有依赖关系的多个模块的编译次序问题等. 假定下图中的 A , B , C , D , K 为待编译的几个模块, 箭头表示依赖关系(如 B , D 依赖于 K ), 经拓扑排序后应输出模块编译顺序, 即 K -> C -> B -> D -> A 或 C -> K -> B -> D -> A ( K 和 C , B 和 D 顺序可互换)

思路

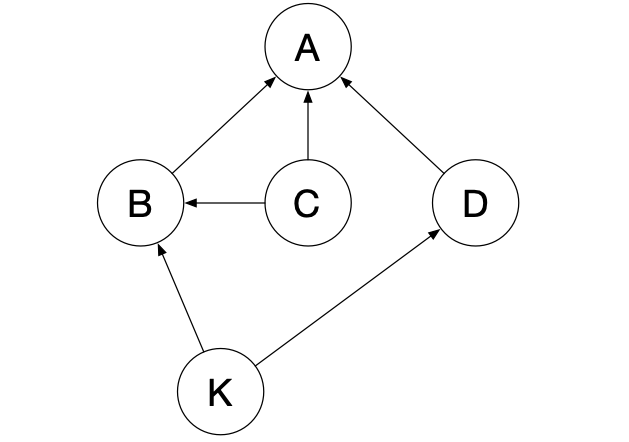
先找到所有入度为 0 的节点并输出, 删除这些节点. 在下一次迭代中, 找到剩余节点中入度为 0 的节点并输出, 直到图中节点全部输出为止.

Java

图的结构定义及实现见另一篇博客

public class TopologySort {
    public static List<GraphNode> topologySort(Graph graph) {
        HashMap<GraphNode, Integer> inMap = new HashMap<>();
        Queue<GraphNode> zeroInQueue = new LinkedList<>();
        // 取出所有节
        for (GraphNode node : graph.nodes.values()) {
            inMap.put(node, node.in);   // 建立节点和其入度的对应关系
            if (node.in == 0)
                zeroInQueue.add(node);
        }

        List<GraphNode> result = new ArrayList<>();
        while (!zeroInQueue.isEmpty()) {
            GraphNode cur = zeroInQueue.poll();
            result.add(cur);
            // 将入度为 0 的节点的下一层节点的入度减一, 若为 0 则放入 zeroInQueue 中
            for (GraphNode next : cur.nexts) {
                inMap.put(next, inMap.get(next) - 1);
                if (inMap.get(next) == 0) {
                    zeroInQueue.add(next);
                }
            }
        }
        return result;
    }
}

Python

def topology_sort(graph):
    in_dict = dict()
    zero_in_list = []

    for node in graph.nodes.values():
        in_dict[node] = node.in_degree
        if node.in_degree == 0:
            zero_in_list.append(node)

    result = []
    while zero_in_list:
        cur = zero_in_list.pop()
        result.append(cur)

        for next in cur.nexts:
            in_dict[next] = in_dict[next] - 1
            if in_dict[next] == 0:
                zero_in_list.append(next)

    return result

深度优先遍历

Posted on 2020-06-21 Edited on 2022-07-20

借助栈和集合实现树和图的深度优先遍历, 每次从栈中取出一个节点 A , 遍历与节点 A 相邻的后续节点 Bn , 若集合中没有该后续 Bn 则将节点 A 放回栈中, 并将后续节点 Bn 放入栈和集合中, 输出后续节点 Bn . 每遍历完一个后续节点就跳出当前循环, 避免出现横向遍历 ( 如下图, 可能会产生 2, 3, 4 的错误输出 ).

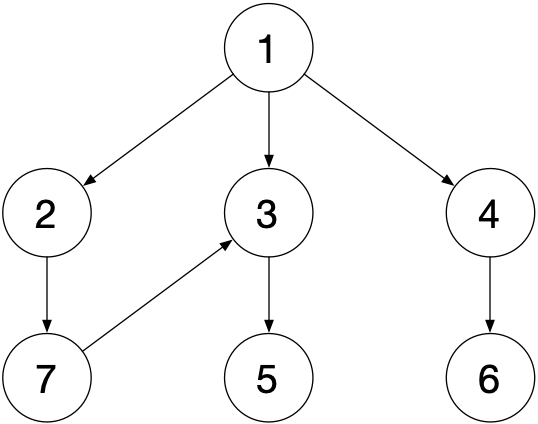
以上图为例, 图的节点定义及整体结构见上一篇博客

Java

public class DFS {
    public static void dfs(GraphNode node) {
        if (node == null) return;

        Stack<GraphNode> stack = new Stack<>();
        HashSet<GraphNode> set = new HashSet<>();
        stack.push(node);
        set.add(node);
        System.out.print(node.value + " ");
        while (!stack.isEmpty()) {
            GraphNode cur = stack.pop();
            for (GraphNode next : cur.nexts) {
                if (!set.contains(next)) {
                    stack.push(cur);
                    stack.push(next);
                    set.add(next);
                    System.out.print(next.value + " ");
                    break;
                }
            }
        }
    }

    public static void main(String[] args) {
        Integer[][] nodes = {
                {1, 1, 2},
                {1, 1, 3},
                {1, 1, 4},
                {1, 2, 3},
                {1, 2, 7},
                {1, 3, 5},
                {1, 4, 6},
                {1, 7, 3}
        };
        Graph graph = GraphBuilder.createGraph(nodes);
        dfs(graph.nodes.get(1));
    }
}

1	1 2 3 5 7 4 6

Python

def dfs(node):
    if not node: return

    ele_stack = []
    ele_set = set()

    ele_stack.append(node)
    ele_set.add(node)

    print(node.value, end=' ')
    while ele_stack:
        current_node = ele_stack.pop()
        for next_node in current_node.nexts:
            if next_node not in ele_set:
                ele_stack.append(current_node)
                ele_stack.append(next_node)
                ele_set.add(next_node)
                print(next_node.value, end=' ')
                break

广度优先遍历

Posted on 2020-06-20 Edited on 2022-07-20

树和图的广度优先遍历可借助一个队列和一个集合实现. 先将当前节点分别放入队列和集合中, 再依次出队, 出队元素将其下一个节点进队, 迭代即可实现广度优先遍历.

以上图为例, 图的节点定义及整体结构见上一篇博客

Java

public class BFS {
    public static void bfs(GraphNode node) {
        if (node == null) return;

        Queue<GraphNode> queue = new LinkedList<>();
        HashSet<GraphNode> set = new HashSet<>();
        queue.add(node);
        set.add(node);
        while (!queue.isEmpty()) {
            GraphNode curNode = queue.poll();
            System.out.print(curNode.value + " ");
            for (GraphNode next : curNode.nexts) {
                if (!set.contains(next)) {
                    set.add(next);
                    queue.add(next);
                }
            }
        }
    }

    public static void main(String[] args) {
        // 无权重, 假定都为 1
        Integer[][] nodes = {
                {1, 1, 2},
                {1, 1, 3},
                {1, 1, 4},
                {1, 2, 3},
                {1, 2, 7},
                {1, 3, 5},
                {1, 4, 6},
                {1, 7, 3}
        };
        Graph graph = GraphBuilder.createGraph(nodes);
        bfs(graph.nodes.get(1));
    }
}

1	1 2 3 4 7 5 6

Python

from queue import Queue

def bfs(node):
    if not node: return

    ele_queue = Queue()
    ele_set = set()

    ele_queue.put(node)
    ele_set.add(node)

    while ele_queue.qsize() != 0:
        current_node = ele_queue.get()
        print(current_node.value, end=' ')
        for next_node in current_node.nexts:
            if next_node not in ele_set:
                ele_set.add(next_node)
                ele_queue.put(next_node)

图

Posted on 2020-06-20 Edited on 2022-07-20

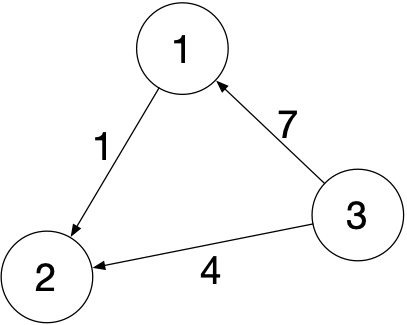
实际开发中常用二维矩阵表示图, 矩阵中的每一行即为一条边, 格式如 [权重, 起始点, 结束点]

[
    [1, 1, 2],
    [4, 3, 2],
    [7, 3, 1]
]

以上矩阵所表示的结构如下:

Java

class GraphNode {
    public int value;   // 值
    public int in = 0;  // 入度
    public int out = 0; // 出度
    public ArrayList<GraphNode> nexts = new ArrayList<>();  // 当前点出发指向的所有相邻节点
    public ArrayList<Edge> edges = new ArrayList<>();       // 从当前点出发的所有边

    public GraphNode(int value) {
        this.value = value;
    }
}

class Edge {
    public int weight;
    public GraphNode from;
    public GraphNode to;

    public Edge(int weight, GraphNode from, GraphNode to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

class Graph {
    public HashMap<Integer, GraphNode> nodes;   // 所有点集, key 为节点编号
    public HashSet<Edge> edges;                 // 所有边集

    public Graph() {
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

public class GraphBuilder {
    public static Graph createGraph(Integer[][] matrix) {
        Graph graph = new Graph();
        for (Integer[] node : matrix) {
            int weight = node[0];
            int from = node[1];
            int to = node[2];
            if (!graph.nodes.containsKey(from)) {
                graph.nodes.put(from, new GraphNode(from));
            }
            if (!graph.nodes.containsKey(to)) {
                graph.nodes.put(to, new GraphNode(to));
            }
            GraphNode fromNode = graph.nodes.get(from);
            GraphNode toNode = graph.nodes.get(to);
            Edge newEdge = new Edge(weight, fromNode, toNode);
            fromNode.nexts.add(toNode);
            fromNode.edges.add(newEdge);
            fromNode.out++;
            toNode.in++;
            graph.edges.add(newEdge);
        }
        return graph;
    }
}

Python

class GraphNode:
    def __init__(self, value):
        self.value = value
        self.in_degree = 0
        self.out_degree = 0
        self.nexts = []
        self.edges = []


class Edge:
    def __init__(self, weight, from_node, to_node):
        self.weight = weight
        self.from_node = from_node
        self.to_node = to_node


class Graph:
    def __init__(self):
        self.nodes = dict()
        self.edges = set()


def create_graph(matrix):
    graph = Graph()
    for node in matrix:
        weight = node[0]
        from_val = node[1]
        to_val = node[2]
        
        if from_val not in graph.nodes.keys():
            graph.nodes[from_val] = GraphNode(from_val)
        if to_val not in graph.nodes.keys():
            graph.nodes[to_val] = GraphNode(to_val)
            
        from_node = graph.nodes.get(from_val)
        to_node = graph.nodes.get(to_val)
        new_edge = Edge(weight, from_node, to_node)
        
        from_node.nexts.append(to_node)
        from_node.edges.append(new_edge)
        from_node.out_degree += 1
        to_node.in_degree += 1
        graph.edges.add(new_edge)

    return graph