Leaky Cauldron
0%

Posted on Edited on

题目(LeetCode #8)

请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。接下来的转化规则如下：

  • 如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。

  • 假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。

  • 该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0 。

提示：

  • 本题中的空白字符只包括空格字符 ' ' 。
  • 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

示例 1:

输入: “42”
输出: 42

示例 2:

输入: “ -42”
输出: -42
解释: 第一个非空白字符为 ‘-‘, 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

输入: “4193 with words”
输出: 4193
解释: 转换截止于数字 ‘3’ ，因为它的下一个字符不为数字。

示例 4:

输入: “words and 987”
输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。
因此无法执行有效的转换。

示例 5:

输入: “-91283472332”
输出: -2147483648
解释: 数字 “-91283472332” 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。

题解

逐位处理字符串，根据每位字符确定一个覆盖所有情况的有限状态机，如下图所示（图源）：

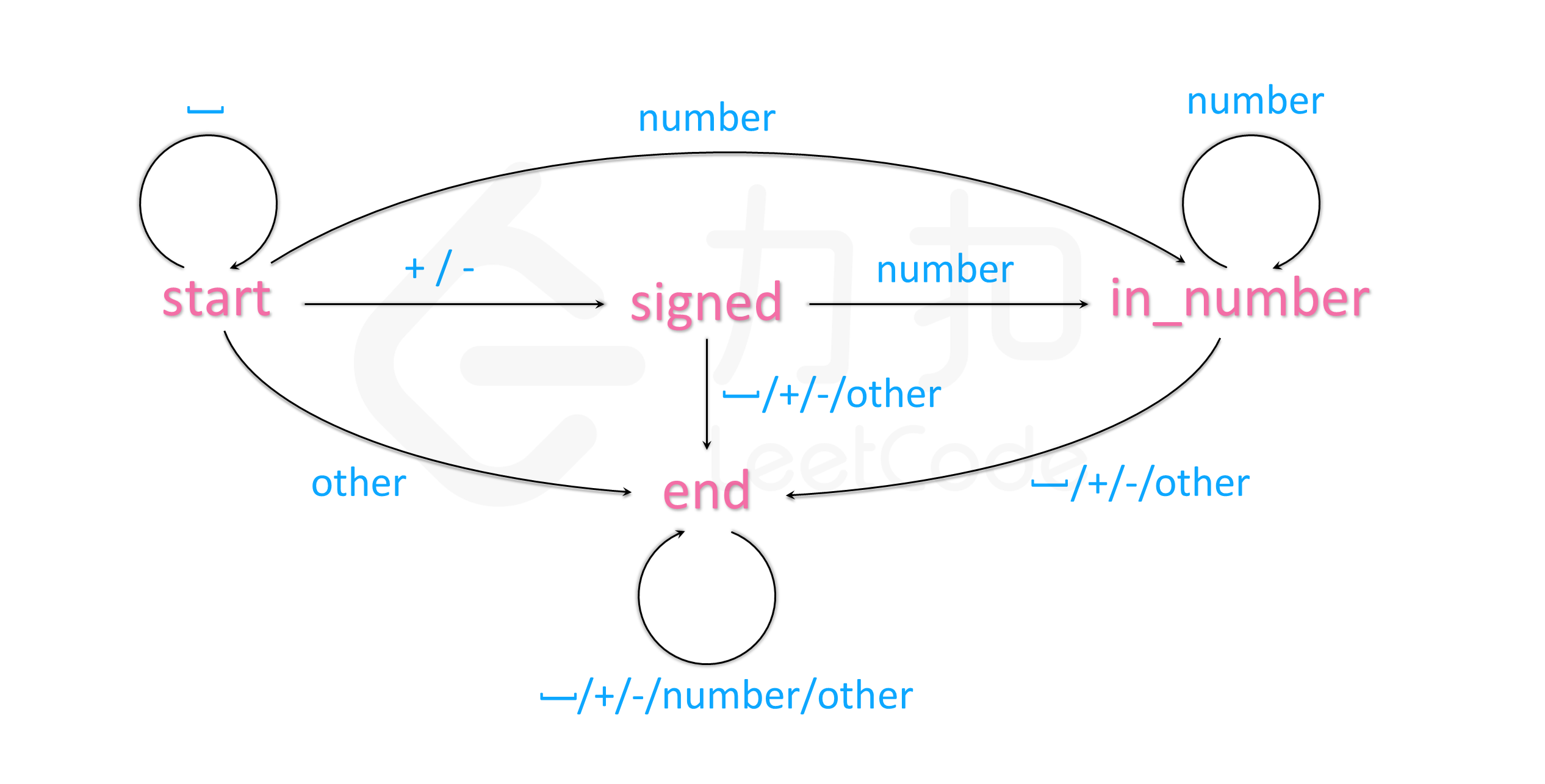
得到以下的状态转移表：

space + / - number other
start start signed in_number end
signed end end in_number end
in_number end end in_number end
end end end end end

根据上表即可编写代码即可

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class FSM {
    public String status = "start";
    public int sign = 1;
    public long ans = 0;
    public HashMap<String, String[]> table = new HashMap<>();

    public FSM() {
        table.put("start", new String[]{"start", "signed", "in_number", "end"});
        table.put("signed", new String[]{"end", "end", "in_number", "end"});
        table.put("in_number", new String[]{"end", "end", "in_number", "end"});
        table.put("end", new String[]{"end", "end", "end", "end"});
    }

    public int getColumn(char ch) {
        if (ch == ' ') return 0;
        if (ch == '+' || ch == '-') return 1;
        if (ch >= '0' && ch <= '9') return 2;
        return 3;
    }

    public void get(char ch) {
        status = table.get(status)[getColumn(ch)];
        if (status.equals("in_number")) {
            int curInt = Character.getNumericValue(ch);
            ans = ans * 10 + curInt;
            if ((int) ans != ans) {
                if (sign == 1) ans = Integer.MAX_VALUE;
                if (sign == -1) ans = Integer.MIN_VALUE;
            }
        } else if (status.equals("signed")) {
            sign = ch == '+' ? 1 : -1;
        }
    }
}

class Solution {
    public int myAtoi(String str) {
        FSM fsm = new FSM();
        for (char ch : str.toCharArray()) {
            fsm.get(ch);
        }
        return fsm.sign * (int) fsm.ans;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class FSM:
    def __init__(self):
        self.state = 'start'
        self.sign = 1
        self.ans = 0
        self.table = {
            'start': ['start', 'signed', 'in_number', 'end'],
            'signed': ['end', 'end', 'in_number', 'end'],
            'in_number': ['end', 'end', 'in_number', 'end'],
            'end': ['end', 'end', 'end', 'end'],
        }

    def get_column(self, c: str) -> int:
        if c.isspace():
            return 0
        if c in ['+', '-']:
            return 1
        if c.isdigit():
            return 2
        return 3

    def get(self, c: str):
        self.state = self.table[self.state][self.get_column(c)]
        if self.state == 'in_number':
            self.ans = self.ans * 10 + int(c)
            self.ans = min(self.ans, INT_MAX) if self.sign == 1 else min(self.ans, -INT_MIN)
        elif self.state == 'signed':
            self.sign = 1 if c == '+' else -1


class Solution:
    def myAtoi(self, str: str) -> int:
        fsm = FSM()
        for c in str:
            fsm.get(c)
        return fsm.sign * fsm.ans

Posted on Edited on

题目(LeetCode #3)

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2:

输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。

示例 3:

输入: “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。答案必须是子串的长度，”pwke” 是一个子序列，不是子串。

题解

可采用滑动窗口法，将窗口内的字符保存到集合中，窗口的左边界向右移动时，弹出已不在窗口内的元素；窗口的右边界向右移动时判断字符是否已在集合中，若不在则加入，若已有则终止循环，记录当前最长长度。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import java.util.HashSet;

public class Solution {
    public int lengthOfLongestSubstring(String s) {
        HashSet<Character> charSet = new HashSet<>();
        int length = s.length();
        int rk = -1, ans = 0;

        for (int i = 0; i < length; i++) {
            if (i != 0) {
                charSet.remove(s.charAt(i - 1));
            }
            while (rk + 1 < length && !charSet.contains(s.charAt(rk + 1))) {
                charSet.add(s.charAt(rk + 1));
                rk++;
            }
            ans = Math.max(ans, rk - i + 1);
        }

        return ans;
    }

    public static void main(String[] args) {
        String s = "abcabcbb";
        Solution solution = new Solution();
        System.out.println(solution.lengthOfLongestSubstring(s));
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        char_set = set()
        rk, ans = -1, 0
        length = len(s)

        for i in range(length):
            if i != 0: char_set.remove(s[i - 1])

            while rk + 1 < length and s[rk + 1] not in char_set:
                char_set.add(s[rk + 1])
                rk += 1
            ans = max(ans, rk - i + 1)

        return ans

Go

Golang 中没有集合，使用 map 实现过于繁琐，可采用 int 数组来模拟集合操作。

将每个字符的 ASCII 值作为数组的索引，数组内存储的为该字符的出现与否（1 或 0）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
package main

import (
	"fmt"
	"math"
)

func lengthOfLongestSubstring(s string) int {
	var window [128]int         // ASCII 总共定义了 128 个字符
	length := len(s)
	rk, ans := -1, 0

	for i, _ := range s {
		if i != 0 {
			window[s[i-1]] = 0  // 左边界移出窗口
		}
		for rk+1 < length && window[s[rk+1]] == 0 {
			window[s[rk+1]] = 1 // 右边界移入窗口
			rk++
		}
		ans = int(math.Max(float64(ans), float64(rk-i+1)))
	}
	return ans
}

Posted on Edited on

定义

二叉查找树，也称为二叉搜索树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

  1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
  3. 任意节点的左、右子树也分别为二叉查找树；

其优势在于查找、插入的时间复杂度较低，理想情况下为 O(logn) 。

实现

节点定义

1
2
3
4
5
6
7
8
9
10
11
12
13
class Node {
    int value;
    Node parent;
    Node left;
    Node right;

    public Node(int value, Node parent, Node left, Node right) {
        this.value = value;
        this.parent = parent;
        this.left = left;
        this.right = right;
    }
}

查找节点

1
2
3
4
5
6
7
8
9
10
11
12
13
public static Node search(int ele) {
    Node tmp = root;

    while (tmp != null && tmp.value != ele) {
        if (ele < tmp.value) {
            tmp = tmp.left;
        } else {
            tmp = tmp.right;
        }
    }

    return tmp;
}

插入节点

先找到待插入节点的父节点，再插入新节点并返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static Node insert(int ele) {
    if (root == null) {
        root = new Node(ele, null, null, null);
        return root;
    }

    // 找到即将插入元素的父节点
    Node parent = null;
    Node tmp = root;
    while (tmp != null) {
        parent = tmp;
        if (ele < tmp.value) {
            tmp = tmp.left;
        } else {
            tmp = tmp.right;
        }
    }

    Node newNode = new Node(ele, parent, null, null);
    if (parent.value > ele) {
        parent.left = newNode;
    } else {
        parent.right = newNode;
    }

    return newNode;
}

删除节点

替换 / 移植节点

使用 newNode 替换 nodeToReplace ，并返回被替换的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static Node transplant(Node nodeToReplace, Node newNode) {
    if (nodeToReplace.parent == null) {
        root = newNode;
    } else if (nodeToReplace == nodeToReplace.parent.left) {
        nodeToReplace.parent.left = newNode;
    } else {
        nodeToReplace.parent.right = newNode;
    }

    if (newNode != null) {
        newNode.parent = nodeToReplace.parent;
    }

    return newNode;
}

找到后继节点

找到节点的中序后继，即该节点右子树上的最小值。

1
2
3
4
5
6
7
public static Node getMinimum(Node node) {
    while (node.left != null) {
        node = node.left;
    }

    return node;
}

删除

将待删除节点的中序后继移动到待删除节点位置，并调整树的结构

  • 若待删除节点的父节点无左子树或右子树，直接将该节点的右子树或左子树上移即可；

  • 若待删除节点的左右子树均不为空，以下图所示树为例，其中 9 为待删除节点，此时其中序后继 10 与 9 不直接相连

    • 先找到待删除节点的中序后继，在此为 10，即为待删除节点的替换节点，此时该后继不与待删除节点直接相连，先将其子树 11 移至 10 位置。①使 successorNode.right 指向待删除节点 9 的 right ，②使 successorNode.right.parent 指向 10，得到：

    • 再将 successorNode 移到 deleteNode 的位置，并修改其左子树的指向。

  • 若中序后继与待删除节点直接相连，如下图所示：

    • 9 与 12 直接相连，则直接将 12 上移至 9 的位置，并修改 12 的左子树指向即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static Node delete(Node deleteNode) {
    if (deleteNode != null) {
        Node nodeToReturn = null;
        if (deleteNode.left == null) {
            nodeToReturn = transplant(deleteNode, deleteNode.right);
        } else if (deleteNode.right == null) {
            nodeToReturn = transplant(deleteNode, deleteNode.left);
        } else {
            Node successorNode = getMinimum(deleteNode.right);
            if (successorNode.parent != deleteNode) {
                transplant(successorNode, successorNode.right);
                successorNode.right = deleteNode.right;
                successorNode.right.parent = successorNode;
            }
            transplant(deleteNode, successorNode);
            successorNode.left = deleteNode.left;
            successorNode.left.parent = successorNode;
            nodeToReturn = successorNode;
        }
        return nodeToReturn;
    }
    return null;
}

缺点

插入或删除节点过程中如果不及时调整，将使查找效率降低，如将数组 [2, 3, 4, 5, 6] 插入树的过程中，不加调整将得到如下结构，此时查找和插入效率退化至 O(n) 。

为解决查找效率退化的问题，又提出了 AVL 树和红黑树等，可将最坏效率降至 O(logn)。

完整代码

Posted on Edited on

原理

无论是手动创建栈遍历树还是递归（即调用系统栈）遍历树，其空间复杂度均为 O(N) ，而 Morris 实现了 O(1) 常数空间复杂度的树的遍历。

递归遍历树的过程中，每个节点均被遍历了三次，前中后序取决于打印的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class RecursiveTraversal {
    public static void recursiveTraverse(TreeNode head) {
        if (head == null) return;

        // 先序遍历
        // System.out.println(head.val);

        recursiveTraverse(head.left);

        // 中序遍历
        // System.out.println(head.val);
        
        recursiveTraverse(head.right);
        
        // 后序遍历
        // System.out.println(head.val);
    }
}

Morris 遍历实质上是人为地追踪递归过程中遍历位置的变化。其过程如下：

设 cur 为当前节点。

  1. 若 cur 无左子树，cur 向右移动
  2. 若 cur 有左子树，找到左子树上最右节点，记为 rightmost
    1. 若 rightmost 的右孩子为 null ，rightmost.right = cur ，cur 向左移动
    2. 若 rightmost 的右孩子为 cur ，rightmost.right = null ，cur 向右移动

  • 若某节点有左子树，则该节点将被遍历两次（即 2.2 ），若没有左子树则将被遍历一次；

  • 在第二遍历某节点时，当前节点总是该节点左子树的 rightmost 的后继（节点的后继指中序遍历输出结果的后续节点）

  • 通过 rightmost 的右孩子的指向来判断是第一次还是第二次遍历到当前节点。

下图为每一步迭代的结果（从左至右，从上到下），cur代表当前节点，深色节点表示该节点已输出。（图源：AnnieKim）

实现

先序遍历

第一次到达一个节点时就输出。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class MorrisTraversal {
    public static void morrisPreorderTraverse(TreeNode head) {
        if (head == null) return;

        TreeNode cur1 = head;
        TreeNode cur2 = null;

        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {                       // cur1 有左子树
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;                // 左子树上最右节点, 此时 cur2 即为 rightmost
                }
                if (cur2.right == null) {             // rightmost 的右孩子为空, 此时为第一次遍历当前节点
                    cur2.right = cur1;
                    System.out.print(cur1.val + " "); // 第一次遍历一个节点, 打印该节点
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;                // rightmost 的右孩子指向 cur1, 此时为第二次遍历当前节点
                }
            } else {
                System.out.print(cur1.val + " ");     // 节点无左子树, 只会遍历一遍, 故直接输出
            }
            cur1 = cur1.right;                        // cur1 无左子树或 rightmost 的右孩子指向 cur1 时
        }
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


def morris_preorder_traverse(head: TreeNode) -> None:
    if not head: return

    cur1 = head
    while cur1:
        cur2 = cur1.left
        if cur2:
            while cur2.right and cur2.right != cur1:
                cur2 = cur2.right
            if cur2.right is None:
                cur2.right = cur1
                print(cur1.val, end=" ")
                cur1 = cur1.left
                continue
            else:
                cur2.right = None
        else:
            print(cur1.val, end=" ")
        cur1 = cur1.right

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
type TreeNode struct {
	val   int
	left  *TreeNode
	right *TreeNode
}

func morrisPreorderTraverse(head *TreeNode) {
	if head == nil {
		return
	}

	cur1 := head
	var cur2 *TreeNode

	for cur1 != nil {
		cur2 = cur1.left
		if cur2 != nil {
			for cur2.right != nil && cur2.right != cur1 {
				cur2 = cur2.right
			}
			if cur2.right == nil {
				cur2.right = cur1
				fmt.Printf("%d ", cur1.val)
				cur1 = cur1.left
				continue
			} else {
				cur2.right = nil
			}
		} else {
			fmt.Printf("%d ", cur1.val)
		}
		cur1 = cur1.right
	}
}

中序遍历

有左子树的节点第二次回到该节点时再打印；无左子树的节点只会遍历一次，故直接输出。如下图输出顺序为 2 1 3 。

当前节点无左子树或第二次遍历当前节点（即 rightmost 的右孩子指向 cur1）时均需输出当前节点值，而只有这两种情况需将指针右移，故可理解为只要向右移动就输出。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class MorrisTraversal {
    public static void morrisInOrderTraverse(TreeNode head) {
        if (head == null) return;

        TreeNode cur1 = head;
        TreeNode cur2 = null;

        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {               // cur1 有左子树
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;        // 左子树上最右节点, 此时 cur2 即为 rightmost
                }
                if (cur2.right == null) {     // rightmost 的右孩子为空, 此时为第一次遍历当前节点
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;        // rightmost 的右孩子指向 cur1, 此时为第二次遍历当前节点
                }
            }
            System.out.print(cur1.val + " "); // 当前节点无左子树或第二次遍历当前节点
            cur1 = cur1.right;                // cur1 无左子树或 rightmost 的右孩子指向 cur1 时
        }
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def morris_in_order_traverse(head: TreeNode) -> None:
    if not head: return

    cur1 = head
    while cur1:
        cur2 = cur1.left
        if cur2:
            while cur2.right and cur2.right != cur1:
                cur2 = cur2.right
            if cur2.right is None:
                cur2.right = cur1
                cur1 = cur1.left
                continue
            else:
                cur2.right = None
        print(cur1.val, end=" ")
        cur1 = cur1.right

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func morrisInOrderTraverse(head *TreeNode) {
	if head == nil {
		return
	}

	cur1 := head
	var cur2 *TreeNode

	for cur1 != nil {
		cur2 = cur1.left
		if cur2 != nil {
			for cur2.right != nil && cur2.right != cur1 {
				cur2 = cur2.right
			}
			if cur2.right == nil {
				cur2.right = cur1
				cur1 = cur1.left
				continue
			} else {
				cur2.right = nil
			}
		}
		fmt.Printf("%d ", cur1.val)
		cur1 = cur1.right
	}
}

后序遍历

第二次遍历到某节点时，逆序打印其左子树的右边界。遍历完后再逆序打印整棵树的右边界即为后序遍历。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class MorrisTraversal {
    public static void morrisPostOrderTraverse(TreeNode head) {
        if (head == null) return;

        TreeNode cur1 = head;
        TreeNode cur2 = null;

        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {             // cur1 有左子树
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;      // 左子树上最右节点, 此时 cur2 即为 rightmost
                }
                if (cur2.right == null) {   // rightmost 的右孩子为空, 此时为第一次遍历当前节点
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;      // rightmost 的右孩子指向 cur1, 此时为第二次遍历当前节点
                    printEdge(cur1.left);   // 第二次遍历到该节点, 打印左子树的右边界
                }
            }
            cur1 = cur1.right;              // cur1 无左子树
        }
        printEdge(head);                    // 打印整棵树的右边界
    }

    public static void printEdge(TreeNode head) {
        TreeNode tail = reverseEdge(head);
        TreeNode cur = tail;

        while (cur != null) {
            System.out.print(cur.val + " ");
            cur = cur.right;
        }
        recursiveTraverse(tail);
    }

    public static TreeNode reverseEdge(TreeNode from) {
        TreeNode pre = null;
        TreeNode next = null;

        while (from != null) {
            next = from.right;
            from.right = pre;
            pre = from;
            from = next;
        }
        return pre;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def morris_post_order_traverse(head: TreeNode) -> None:
    if not head: return

    cur1 = head
    while cur1:
        cur2 = cur1.left
        if cur2:
            while cur2.right and cur2.right != cur1:
                cur2 = cur2.right
            if cur2.right is None:
                cur2.right = cur1
                cur1 = cur1.left
                continue
            else:
                cur2.right = None
                print_edge(cur1.left)
        cur1 = cur1.right
    print_edge(head)


def print_edge(head: TreeNode) -> None:
    tail = reverse_edge(head)
    cur = tail

    while cur:
        print(cur.val, end=" ")
        cur = cur.right

    reverse_edge(tail)


def reverse_edge(head: TreeNode) -> TreeNode:
    pre = None
    while head:
        rear = head.right
        head.right = pre
        pre = head
        head = rear
    return pre

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
func morrisPostOrderTraverse(head *TreeNode) {
	if head == nil {
		return
	}

	cur1 := head
	var cur2 *TreeNode

	for cur1 != nil {
		cur2 = cur1.left
		if cur2 != nil {
			for cur2.right != nil && cur2.right != cur1 {
				cur2 = cur2.right
			}
			if cur2.right == nil {
				cur2.right = cur1
				cur1 = cur1.left
				continue
			} else {
				cur2.right = nil
				printEdge(cur1.left)
			}
		}
		cur1 = cur1.right
	}
	printEdge(head)
}

func printEdge(head *TreeNode) {
	tail := reverseEdge(head)
	cur := tail

	for cur != nil {
		fmt.Printf("%d ", cur.val)
		cur = cur.right
	}

	reverseEdge(tail)
}

func reverseEdge(head *TreeNode) *TreeNode {
	var pre *TreeNode
	for head != nil {
		next := head.right
		head.right = pre
		pre = head
		head = next
	}

	return pre
}

Posted on Edited on

题目(LeetCode #215)

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

题解

参考资料：

https://segmentfault.com/a/1190000008322873

https://www.jianshu.com/p/a43b0e1712d1

https://www.cnblogs.com/ldy-miss/p/12031077.html

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
public class BFPRT {
    public static int findKthLargest(int[] arr, int K) {
        int[] copyArr = copyArray(arr);
        return select(copyArr, 0, copyArr.length - 1, K - 1);
    }

    public static int[] copyArray(int[] arr) {
        int[] res = new int[arr.length];
        for (int i = 0; i != res.length; i++) {
            res[i] = arr[i];
        }
        return res;
    }

    public static int select(int[] arr, int begin, int end, int i) {
        if (begin == end) {
            return arr[begin];
        }

        int pivot = medianOfMedians(arr, begin, end);
        int[] pivotRange = partition(arr, begin, end, pivot);
        if (i >= pivotRange[0] && i <= pivotRange[1]) {
            return arr[i];
        } else if (i < pivotRange[0]) {
            return select(arr, begin, pivotRange[0] - 1, i);
        } else {
            return select(arr, pivotRange[1] + 1, end, i);
        }
    }

    public static int medianOfMedians(int[] arr, int begin, int end) {
        int num = end - begin + 1;
        int offset = num % 5 == 0 ? 0 : 1;
        int[] mArr = new int[num / 5 + offset];
        for (int i = 0; i < mArr.length; i++) {
            int beginI = begin + i * 5;
            int endI = beginI + 4;
            mArr[i] = getMedian(arr, beginI, Math.min(end, endI));
        }
        // return getMedian(mArr, 0, mArr.length - 1);
        return select(mArr, 0, mArr.length - 1, mArr.length / 2); // 实测比直接调用 getMedian 更快
    }

    public static int[] partition(int[] arr, int begin, int end, int pivotValue) {
        int small = begin - 1;
        int cur = begin;
        int big = end + 1;
        while (cur != big) {
            if (arr[cur] > pivotValue) {
                swap(arr, ++small, cur++);
            } else if (arr[cur] < pivotValue) {
                swap(arr, cur, --big);
            } else {
                cur++;
            }
        }
        int[] range = new int[2];
        range[0] = small + 1;
        range[1] = big - 1;
        return range;
    }

    public static int getMedian(int[] arr, int begin, int end) {
        insertionSort(arr, begin, end);
        int sum = end + begin;
        int mid = (sum / 2) + (sum % 2);
        return arr[mid];
    }

    public static void insertionSort(int[] arr, int begin, int end) {
        for (int i = begin + 1; i != end + 1; i++) {
            for (int j = i; j != begin; j--) {
                if (arr[j - 1] > arr[j]) {
                    swap(arr, j - 1, j);
                } else {
                    break;
                }
            }
        }
    }

    public static void swap(int[] arr, int index1, int index2) {
        int tmp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = tmp;
    }
}

Posted on Edited on

题目(LeetCode #214)

给定一个字符串 s，你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。

示例 1:

输入: “aacecaaa”
输出: “aaacecaaa”

示例 2:

输入: “abcd”
输出: “dcbabcd”

题解

可利用Manacher 算法找到原字符串包含第一个字符的最长回文子串，将该回文子串后的字符逆序加到开头即可。

示例 1 中，对 aacecaaa 来说，包含第一个字符的最长回文子串为 aacecaa ，需把剩余的 a 逆序加到开头，即得到 aaacecaaa ；示例 2 中，abcd 包含第一个字符的最长回文子串为 a ，bcd 逆序得到 dcb ，放到开头即得到 dcbabcd 。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class ShortestPalindrome {
    public static String preprocess(String s) {
        String result = "^";
        for (int i = 0; i < s.length(); i++) {
            result += "#" + s.charAt(i);
        }

        return result + "#$";
    }

    public static String shortestPalindrome(String s) {
        if (s == null || s.length() == 0) return "";

        String tmpStr = preprocess(s);
        int strLen = tmpStr.length();
        int C = 0, R = 0;
        int[] p = new int[strLen];
        int maxLen = 0;

        for (int i = 1; i < strLen - 1; i++) {
            p[i] = R > i ? Math.min(p[2 * C - i], R - i) : 1;

            while (tmpStr.charAt(i - p[i]) == tmpStr.charAt(i + p[i])) {
                p[i]++;
            }

            if (R < p[i] + i) {
                R = p[i] + i;
                C = i;
            }

            // 仅保存以第一个字符开头的回文子串的最大长度
            // (C - p[C]) / 2 即为当前回文串的起始索引
            if (maxLen < p[i] - 1 && (C - p[C]) / 2 == 0) {
                maxLen = p[i] - 1;
            }
        }

        // 逆序剩余部分字符串
        String result = "";
        for (int i = s.length() - 1; i >= maxLen; i--) {
            result += s.charAt(i);
        }

        return result + s;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class ShortestPalindrome:
    def shortest_palindrome(self, s: str) -> str:
        tmp_str = "^#" + "".join([x + "#" for x in s]) + "$"
        str_len = len(tmp_str)
        p = [0] * str_len
        c, r = 0, 0
        max_len = 0

        for i in range(1, str_len - 1):
            p[i] = min(p[2 * c - i], r - i) if r > i else 1
            while tmp_str[i - p[i]] == tmp_str[i + p[i]]:
                p[i] += 1

            if r < p[i] + i:
                r = p[i] + i
                c = i

            if max_len < p[i] - 1 and (c - p[c]) // 2 == 0:
                max_len = p[i] - 1

        return "".join([x for x in s[:max_len - 1:-1]]) + s

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
func preprocess(s string) string {
	result := "^#"

	for _, ch := range s {
		result += string(ch) + "#"
	}

	return result + "$"
}

func shortestPalindrome(s string) string {
	if len(s) == 0 {
		return ""
	}

	tmpStr := preprocess(s)
	strLen := len(tmpStr)
	p := make([]int, strLen)
	C, R := 0, 0
	maxLen := 0

	for i := 1; i < strLen-1; i++ {
		if R > i {
			p[i] = min(p[2*C-i], R-i)
		} else {
			p[i] = 1
		}

		for tmpStr[i-p[i]] == tmpStr[i+p[i]] {
			p[i]++
		}

		if R < p[i]+i {
			R = p[i] + i
			C = i
		}

		if maxLen < p[i]-1 && (C-p[C])/2 == 0 {
			maxLen = p[i] - 1
		}
	}

	result := ""
	for i := len(s) - 1; i >= maxLen; i-- {
		result += string(s[i])
	}

	return result + s
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

Posted on Edited on

题目(LeetCode #5)

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：

输入: “cbbd”
输出: “bb”

题解

扩展中心法

遍历字符串，由每个字符串向两侧扩展逐一比对。

时间复杂度为 O(n²) 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() <= 1) return s;

        int begin = 0, maxLen = 1;
        for (int i = 0; i < s.length(); i++) {
            int oddLen = expandAroundCenter(s, i, i);
            int evenLen = expandAroundCenter(s, i, i + 1);
            int curLen = Math.max(oddLen, evenLen);

            if (curLen > maxLen) {
                maxLen = curLen;
                begin = i - (maxLen - 1) / 2; // (maxLen - 1) / 2 向下取整
            }
        }

        return s.substring(begin, begin + maxLen);
    }

    private int expandAroundCenter(String s, int l, int r) {
        while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
            l--; r++;
        }

        return r - l - 1; // 此时 l 指向回文子串前一位，r 指向回文子串后一位
    }
}

Manacher算法

预处理

在原始字符串的每个字符的左右两边都加上特殊字符，使处理后的字符串长度均为奇数，以此来解决偶回文时用扩展法不能找到回文中心而导致的找不到回文子串的问题。

处理前

处理后

最长回文子串长度

下表中 p 数组存储的是以各字符为中心的回文子串的最大长度。观察可知，预处理后的字符串的最长回文子串的回文半径减 1 即为原字符串的最长回文子串长度。以字符串 cabbaf 为例，处理后的最长回文子串的回文半径为 p[6] = 5 ，p[6] - 1 = 4 即为原字符串的最长回文子串 abba 的长度。

所以原字符串的最长回文子串长度 maxLen = p[i] - 1

最长回文子串的起始索引

在 #c#a#b#b#a#f# 中，p[6] = 5 ，用索引 i 减去最长回文半径 p[i] 即可得到原字符串的最长回文子串的起始索引，即 i - p[i] = 6 - 5 = 1 ；但对奇回文 aba 来说，用这种方法得到的结果为 3 - p[3] = 3 - 4 = -1 ，下标越界。

为解决下标越界的问题，可在预处理后的字符串前再添加一个特殊字符，而为了使字符串长度保持为奇数，其后也需添加另一个字符。而原字符串的最长回文子串的起始索引变为 (i - p[i]) / 2 。

对 cabbaf 来说，原字符串的最长回文子串的起始索引为 (7 - p[7]) / 2 = (7 - 5) / 2 = 1

对 aba 来说，原字符串的最长回文子串的起始索引为 (3 - p[3]) / 2 = (3 - 3) / 2 = 0

故原字符串的最长回文子串的起始索引可表示为 index = (i - p[i]) / 2

计算 p 数组

定义两个变量 C 和 R ，分别为某一回文子串的中心字符的索引和右边界。如对 ^#c#a#b#b#a#f#$ 中的 #a#b#b#a# 来说，C = 7 ，p[C] = 5 ，以 7 为中心的回文子串的右边界即为 R = C + p[C] = 12 ；当 C = 12 时，以 12 为中心的回文子串的右边界即为 R = C + p[C] = 12 + 2 = 14 。

故可得回文子串右边界与其半径之间的关系为：R = C + p[C]

由于回文子串关于 C 对称，由该子串上某位置 i 可得其对称位置 j ，由 i + j = 2 * C 知 j = 2 * C - i 。

  • 若以 j 为中心的回文子串的右边界在 R 以内，即 j + p[j] < R 时，由对称性可知，p[j] = p[i] ；
  • 若以 j 为中心的回文子串的右边界大于 R ，即 j + p[j] > R 时，图中红色部分为关于 j 对称的回文子串，故此时有 p[j] = R - j ；
  • 若 j + p[j] >= R ，则令 p[j] = 1 ，此时也需更新 C 和 R ，继续向后用扩展中心法计算 p 各位置的值。
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class Manacher {
    public String preprocess(String s) {
        String result = "^";
        for (int i = 0; i < s.length(); i++) {
            result += "#" + s.charAt(i);
        }

        return result + "#$";
    }

    public String longestPalindrome(String s) {
        if (s.length() == 0) return "";

        String tmpStr = preprocess(s);
        int len = tmpStr.length();
        int[] p = new int[len];
        int C = 0, R = 0;
        int maxLen = -1;    // 最长回文子串长度
        int index = 0;      // 最长回文子串中心索引

        for (int i = 1; i < len - 1; i++) {
            p[i] = R > i ? Math.min(p[2 * C - i], R - i) : 1;

            while (tmpStr.charAt(i + p[i]) == tmpStr.charAt(i - p[i]))
                p[i]++;

            if (R < p[i] + i) {
                R = p[i] + i;
                C = i;
            }

            if (maxLen < p[i] - 1) {
                maxLen = p[i] - 1;
                index = i;
            }
        }

        int start = (index - maxLen) / 2;   // (i - p[i]) / 2
        return s.substring(start, start + maxLen);
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Manacher:
    def longest_palindrome(self, s: str) -> str:
        if s is None or len(s) == 0: return ""

        tmp_str = '^#' + ''.join([x + '#' for x in s]) + "$"
        length = len(tmp_str)
        p = [0] * length
        c, r = 0, 0
        max_len = -1
        index = 0

        for i in range(1, length - 1):
            p[i] = min(p[2 * c - i], r - i) if r > i else 1

            while tmp_str[i + p[i]] == tmp_str[i - p[i]]:
                p[i] += 1

            if r < i + p[i]:
                r = i + p[i]
                c = i

            if max_len < p[i] - 1:
                max_len = p[i] - 1
                index = i

        start = (index - max_len) // 2
        return s[start: start + max_len]
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
func preprocess(s string) string {
	result := "^#"

	for _, ch := range s {
		result += string(ch) + "#"
	}

	return result + "$"
}

func longestPalindrome(s string) string {
	if len(s) == 0 {
		return ""
	}

	tmpStr := preprocess(s)
	length := len(tmpStr)
	p := make([]int, length)
	C, R := 0, 0
	maxLen := 0
	index := 0

	for i := 1; i < length-1; i++ {
		if R > i {
			p[i] = int(math.Min(float64(p[2*C-i]), float64(R-i)))
		} else {
			p[i] = 1
		}

		for tmpStr[i+p[i]] == tmpStr[i-p[i]] {
			p[i]++
		}

		if R < i+p[i] {
			R = i + p[i]
			C = i
		}

		if maxLen < p[i]-1 {
			maxLen = p[i] - 1
			index = i
		}
	}

	start := (index - maxLen) / 2
	return s[start : start+maxLen]
}

参考资料

马拉车算法

leetcode.wang

Posted on Edited on

题目(LeetCode #572)

给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。

示例 1:

给定的树 s:

1
2
3
4
5
    3
   / \
  4   5
 / \
1   2

给定的树 t：

1
2
3
  4 
 / \
1   2

返回 true，因为 t 与 s 的一个子树拥有相同的结构和节点值。

示例 2:

给定的树 s：

1
2
3
4
5
6
7
    3
   / \
  4   5
 / \
1   2
   /
  0

给定的树 t：

1
2
3
  4
 / \
1   2

返回 false。

题解

仅作为KMP的练习，非最优解

先将两棵树序列化（这里采用先序遍历），再利用 KMP 判断 t 是否为 s 的子串。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class Code_45_SubtreeOfAnotherTree {
    public static String getPreorderString(TreeNode treeNode) {
        if (treeNode == null) return "#";

        String tmpResult = "_" + treeNode.val + "_" + getPreorderString(treeNode.left);
        tmpResult += "_" + getPreorderString(treeNode.right);

        return tmpResult;
    }

    public static int[] getNextTable(String pattern) {
        int len = pattern.length();
        int lp = -1, rp = 0;
        int[] nextTable = new int[len];
        nextTable[0] = -1;

        while (rp < len - 1) {
            if (lp == -1 || pattern.charAt(lp) == pattern.charAt(rp)) {
                nextTable[++rp] = ++lp;
            } else {
                lp = nextTable[lp];
            }
        }

        return nextTable;
    }

    // KMP
    public static boolean isSubtree(TreeNode s, TreeNode t) {
        String serializedS = getPreorderString(s);
        String serializedT = getPreorderString(t);
        int sCur = 0, tCur = 0;
        int sLen = serializedS.length();
        int tLen = serializedT.length();
        int[] nextTable = getNextTable(serializedT);

        while (sCur < sLen && tCur < tLen) {
            if (serializedS.charAt(sCur) == serializedT.charAt(tCur)) {
                sCur++;
                tCur++;
            } else {
                if (tCur == 0) sCur++;
                else tCur = nextTable[tCur];
            }
        }

        return tCur == tLen;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class SubTreeOfAnotherTree:
    def get_preorder_string(self, tree_node: TreeNode):
        if not tree_node: return '#'

        tmp_str = '_' + str(tree_node.val) + '_' + self.get_preorder_string(tree_node.left)
        tmp_str += '_' + self.get_preorder_string(tree_node.right)

        return tmp_str

    def get_next_table(self, pattern: str):
        lp, rp = -1, 0
        length = len(pattern)
        next_table = [0] * length
        next_table[0] = -1

        while rp < length - 1:
            if pattern[lp] == pattern[rp] or lp == -1:
                lp += 1
                rp += 1
                next_table[rp] = lp
            else:
                lp = next_table[lp]

        return next_table

    def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
        serialized_s = self.get_preorder_string(s)
        serialized_t = self.get_preorder_string(t)
        s_len = len(serialized_s)
        t_len = len(serialized_t)

        s_cur, t_cur = 0, 0
        next_table = self.get_next_table(serialized_t)

        while s_cur < s_len and t_cur < t_len:
            if serialized_s[s_cur] == serialized_t[t_cur]:
                s_cur += 1
                t_cur += 1
            else:
                if t_cur == 0:
                    s_cur += 1
                else:
                    t_cur = next_table[t_cur]

        return t_cur == t_len

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func getPreorderString(treeNode *TreeNode) string {
	if treeNode == nil {
		return "#"
	}

	tmpStr := "_" + strconv.Itoa(treeNode.Val) + "_" + getPreorderString(treeNode.Left)
	tmpStr += "_" + getPreorderString(treeNode.Right)

	return tmpStr
}

func getNextTable(pattern string) []int {
	lp, rp := -1, 0
	length := len(pattern)
	nextTable := make([]int, length)
	nextTable[0] = -1

	for rp < length-1 {
		if lp == -1 || pattern[lp] == pattern[rp] {
			lp++
			rp++
			nextTable[rp] = lp
		} else {
			lp = nextTable[lp]
		}
	}

	return nextTable
}

func isSubtree(s *TreeNode, t *TreeNode) bool {
	serializedS := getPreorderString(s)
	serializedT := getPreorderString(t)
	sCur, tCur := 0, 0
	sLen := len(serializedS)
	tLen := len(serializedT)
	nextTable := getNextTable(serializedT)

	for sCur < sLen && tCur < tLen {
		if serializedS[sCur] == serializedT[tCur] {
			sCur++
			tCur++
		} else {
			if tCur == 0 {
				sCur++
			} else {
				tCur = nextTable[tCur]
			}
		}
	}

	return tCur == tLen
}

奇淫巧技

LeetCode @洪世贤：
没有什么是 Python 一行解决不了的

Python 的诱惑？

1
2
3
class Solution:
    def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
        return str(s).find(str(t)) != -1