Leaky Cauldron
0%

Posted on Edited on

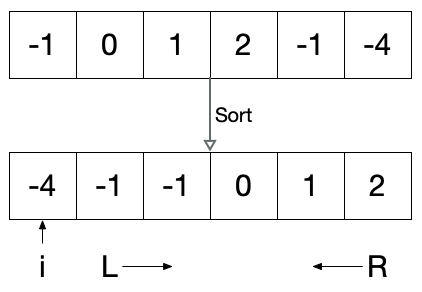
概念

将数组视为哈希表，哈希函数为数组元素与数组索引之间的映射。

例题 1(剑指 offer #03)

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
 [2, 3, 1, 0, 2, 5, 3]
输出： 2 或 3

限制：

2 <= n <= 100000

题解

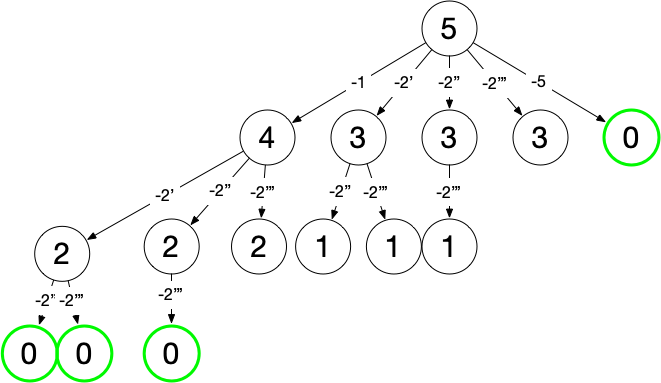
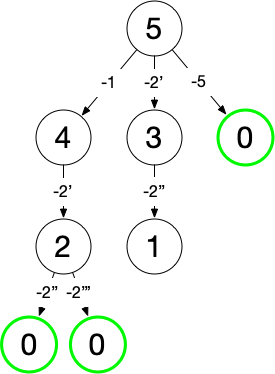
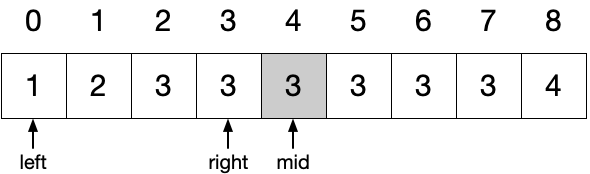
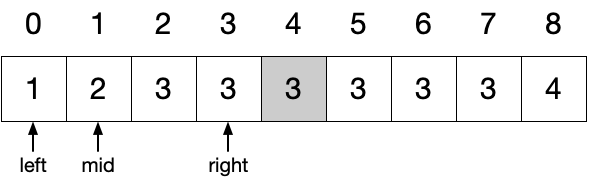
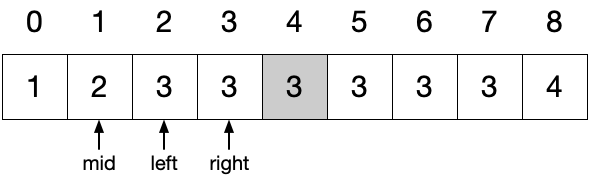
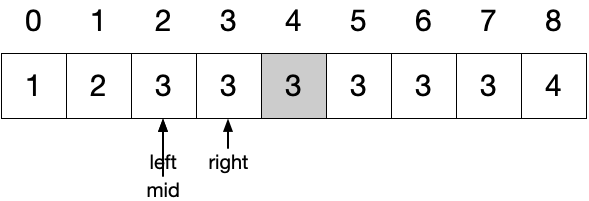
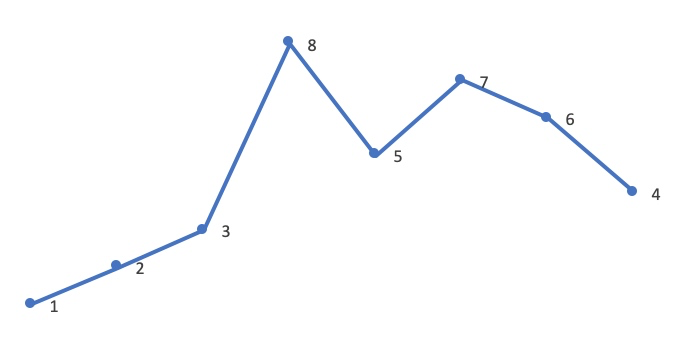
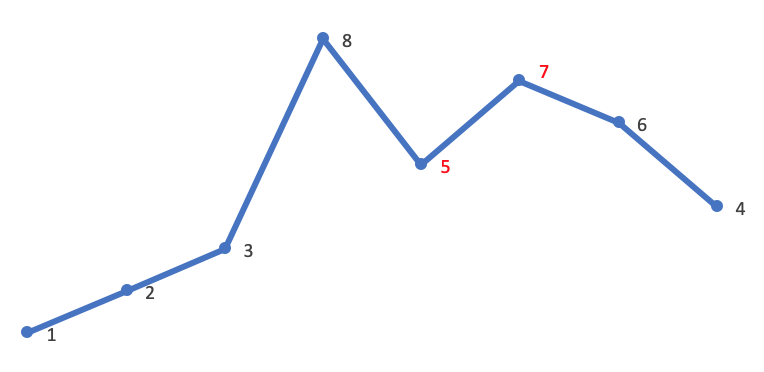
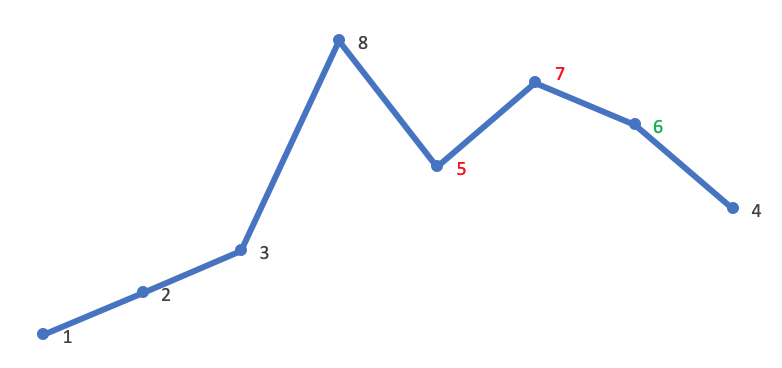
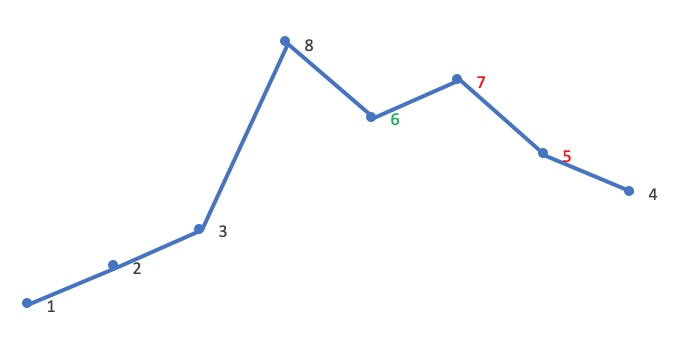
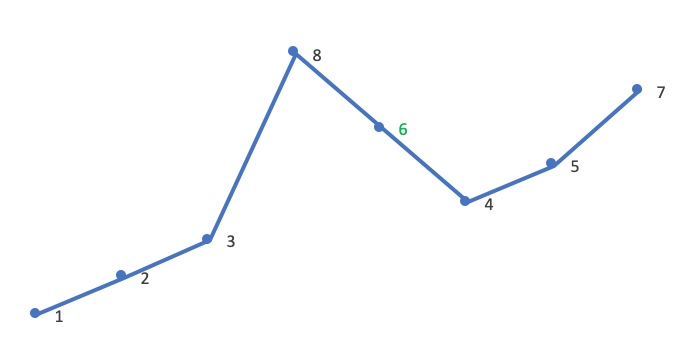
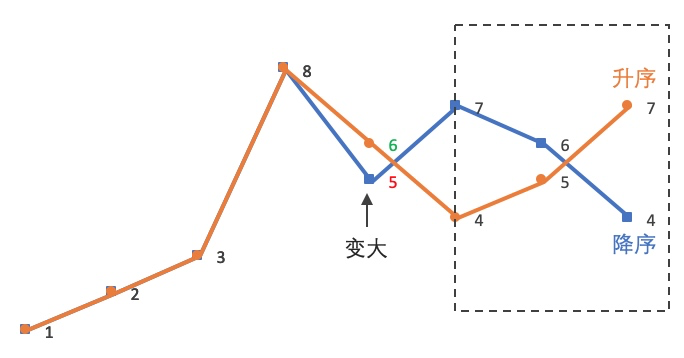
将数组中各元素放至与与元素值相等的索引处（即将数组视为哈希表，哈希函数为 f(nums[i]) = nums[i]），在交换过程中若发现目标位置已有满足条件的值则说明遇到了重复：

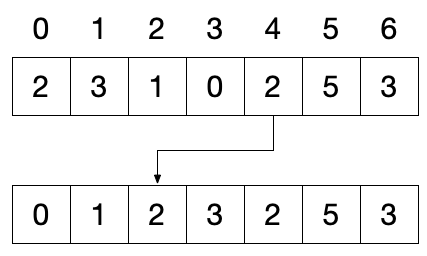
当遍历至 4 位置处的 2 时发现目标位置已有 2，说明 2 发生了重复。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int findRepeatNumber(int[] nums) {
        int tmp;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i) {
                if (nums[i] == nums[nums[i]]) return nums[i];
            }
            tmp = nums[i];
            nums[i] = nums[tmp];
            nums[tmp] = tmp;
        }

        return -1;
    }
}

例题 2 (LeetCode #41)

给你一个未排序的整数数组，请你找出其中没有出现的最小的正整数。

示例 1:

输入: [1, 2, 0]
输出: 3

示例 2:

输入: [3, 4, -1, 1]
输出: 2

示例 3:

输入: [7, 8, 9, 11, 12]
输出: 1

提示：

你的算法的时间复杂度应为 O(n) ，并且只能使用常数级别的额外空间。

题解

本题难在限制了时间复杂度为 O(n) 且常数级别的额外空间，利用排序算法时间复杂度最低为 O(logn) ，不符合条件。

由题意可知，输出的范围为 [1, n + 1] ，将数组视为哈希函数为 f(nums[i]) = nums[i] - 1 的哈希表将数组重新排布。再遍历数组并判断各元素是否满足 nums[i] == i + 1 的对应关系，若不满足则数组中未出现的最小整数为 i + 1 ，若数组中元素全部满足条件则最小整数即为数组长度加 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int firstMissingPositive(int[] nums) {
        int len = nums.length;

        for (int i = 0; i < len; i++) {
            while (nums[i] >= 0 && nums[i] <= len && nums[i] != nums[nums[i] - 1])
                swap(i, nums[i] - 1, nums);
        }

        for (int i = 0; i < len; i++) {
            if (nums[i] != i + 1) return i + 1;
        }

        return len + 1;
    }

    public void swap(int i, int j, int[] nums) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

Posted on Edited on

题目(LeetCode #39)

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

输入： candidates = [2, 3, 6, 7], target = 7,

所求解集为：
[
  [7],
  [2,2,3]
]

示例 2：

输入： candidates = [2,3,5], target = 8,

所求解集为：
[
  [2, 2, 2, 2],
  [2, 3, 3],
  [3, 5]
]

提示：

  • 1 <= candidates.length <= 30
  • 1 <= candidates[i] <= 200
  • candidate 中的每个元素都是独一无二的。
  • 1 <= target <= 500

题解

参考题解

思路分析

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

本题为回溯法经典例题，以 candidates = [2, 3, 6, 7] ， target = 7 为例，可用 target 减去 candidates 中的元素，得到新的 target ，再减去 candidates 中的元素，多次相减，若在某次迭代中 target 变为 0，则减数的集合即为一个解；若 target 小于 0 则回退至上一步继续寻找下一个解。如下图所示，其中绿色叶节点所在的路径即为一解。

以上算法实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import java.util.*;

class Solution {
    List<List<Integer>> results = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int arrLen = candidates.length;
        if (arrLen == 0) return results;

        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, arrLen, target, path);
        return results;
    }

    public void dfs(int[] candidates, int begin, int arrLen, int target, Deque<Integer> path) {
        if (target < 0) return;
        if (target == 0) {
            results.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < arrLen; i++) {
            path.addLast(candidates[i]);
            dfs(candidates, i, arrLen, target - candidates[i], path);
            // 回溯，移除路径的最后一段，相当于回到了上一层。
            // 如路径[2, 2, 2, 2]，上一行 dfs 递归遇到 target < 0，返回。
            // 移除路径最后一段 2，即返回了上一层的 1，继续计算 candidates[i] = 3 的情况。
            path.removeLast();
        }
    }
}

输出：

1
2
3
4
[ 2 2 3 ]
[ 2 3 2 ]
[ 3 2 2 ]
[ 7 ]

可以看到出现了重复解，这是由于每次计算下一层的 target 时均考虑了 candidates 的所有情况。若要避免这种重复，可在每个分支上排除之前已计算过的 candidates 值，如在 7 - 2 = 5 分支上已考虑了所有 candidates[i] = 2 的情况，在 7 - 3/6/7 三个分支上无需重复考虑。去重后树结构如下：

实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import java.util.*;

class Solution {
    List<List<Integer>> results = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int arrLen = candidates.length;
        if (arrLen == 0) return results;

        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, arrLen, target, path);
        return results;
    }

    public void dfs(int[] candidates, int begin, int arrLen, int target, Deque<Integer> path) {
        if (target < 0) return;
        if (target == 0) {
            results.add(new ArrayList<>(path));
            return;
        }

        // 对 candidates 的循环改为从 begin 位置开始
        // 如遍历到 i = 1 时，后续遍历时也会跳过 i = 0 位置
        for (int i = begin; i < arrLen; i++) {
            path.addLast(candidates[i]);
            dfs(candidates, i, arrLen, target - candidates[i], path);
            path.removeLast();
        }
    }
}

此时输出即为无重复的解：

1
2
[ 2 2 3 ]
[ 7 ]

剪枝提速

在计算过程中，若 target 减去某个 candidates[i] 后小于 0，则大于该 candidates[i] 的值与 target 的差也必然小于 0。故可先对 candidates 数组进行升序排序，在遍历 candidates 数组的过程中，若 target < candidates[i] 则 i + 1 及其之后的位置也无需考虑。

注意： 采用这种剪枝方法必须先将 candidates 数组排序，否则若大于 target 的数排在前时，会提前触发 break，导致后边小于 target 的元素被跳过。

剪枝后的树如下，可以看到已减少了很多分支：

实现如下

Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> result = new ArrayList<>();
        if (len == 0) return result;

        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, result);
        return result;
    }

    public void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            if (target < candidates[i]) break;
            path.addLast(candidates[i]);
            dfs(candidates, i, len, target - candidates[i], path, result);
            path.removeLast();
        }
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def __init__(self):
        self.path = []
        self.results = []

    def combinationSum(self, candidates: list, target: int) -> list:
        arr_len = len(candidates)
        if arr_len == 0: return self.results

        candidates.sort()
        self.dfs(candidates, 0, arr_len, target)
        return self.results

    def dfs(self, candidates: list, begin: int, arr_len: int, target: int) -> None:
        if target == 0:
            self.results.append(self.path[:]) # 此处注意需要深拷贝
            return

        for i in range(begin, arr_len):
            if (target - candidates[i] < 0): break
            self.path.append(candidates[i])
            self.dfs(candidates, i, arr_len, target - candidates[i])
            self.path.pop()
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func combinationSum(candidates []int, target int) [][]int {
	arrLen := len(candidates)
	var results [][]int
	if arrLen == 0 {
		return results
	}

	var path []int
	sort.Ints(candidates)
	dfs(candidates, 0, arrLen, target, &results, path)
	return results
}

func dfs(candidates []int, begin, arrLen, target int, results *[][]int, path []int) {
	if target == 0 {
		*results = append(*results, path[:]) // 深拷贝
		return
	}

	for i := begin; i < arrLen; i++ {
		if target - candidates[i] < 0 {
			break
		}

		path = append(path, candidates[i])
		dfs(candidates, i, arrLen, target - candidates[i], results, path)
		path = path[:len(path)-1]
	}
}

进阶(LeetCode #40)

参考题解

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

  • 所有数字（包括目标数）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

输入： candidates = [10, 1, 2, 7, 6, 1, 5], target = 8,

所求解集为：
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2：

输入： candidates = [2, 5, 2, 1, 2], target = 5,

所求解集为：
[
  [1, 2, 2],
  [5]
]

题解

以 candidates = [2, 5, 2, 1, 2] ，target = 5 为例，若采用 #39 题中的算法，得到以下树结构（以 2',2'',2''' 区分三个位置的 2）：

输出如下

1
2
3
4
5
6
7
8
9
10
11
[ 1 1 1 1 1 ]
[ 1 1 1 2 ]
[ 1 1 1 2 ]
[ 1 1 1 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 5 ]

需修改算法使之满足以下两个条件：

  • 每个数字在每个组合中只能使用一次
  • 解集不能包含重复的组合

限制组合中数字的出现次数

在分支上遍历 candidates 时跳过已使用过的位置即可，此时树的结构如下：

实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> result = new ArrayList<>();
        if (len == 0) return result;

        // 必须先排序
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, result);
        return result;
    }

    public void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            if (target < candidates[i]) break;
            path.addLast(candidates[i]);
            // 下一层 begin 从 i + 1 开始，跳过当前的 i
            dfs(candidates, i + 1, len, target - candidates[i], path, result);
            path.removeLast();
        }
    }
}

此时输出为：

1
2
3
4
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 5 ]

去除重复组合

从图中可知组合 [1, 2', 2''] 、[1, 2', 2'''] 和 [1, 2'', 2'''] 三者重复，要去除这种重复应跳过同一层级出现的相等元素。剪枝后的树结构如下：

最终输出为：

1
2
[ 1 2 2 ]
[ 5 ]

实现如下：

Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> result = new ArrayList<>();
        if (len == 0) return result;

        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, result);
        return result;
    }

    public void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            if (target < candidates[i]) break;
            // 跳过同一层的相等元素
            if (i > begin && candidates[i] == candidates[i - 1]) continue;
            path.addLast(candidates[i]);
            dfs(candidates, i + 1, len, target - candidates[i], path, result);
            path.removeLast();
        }
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def __init__(self):
        self.path = []
        self.results = []

    def combinationSum2(self, candidates: list, target: int) -> list:
        arr_len = len(candidates)
        if arr_len == 0: return self.results

        candidates.sort()
        self.dfs(candidates, 0, arr_len, target)

        return self.results

    def dfs(self, candidates: list, begin: int, arr_len: int, target: int) -> None:
        if target == 0:
            self.results.append(self.path[:]) # 注意此处 path 需要深拷贝
            return

        for i in range(begin, arr_len):
            if target - candidates[i] < 0: break
            if i > begin and candidates[i] == candidates[i - 1]: continue
            self.path.append(candidates[i])
            self.dfs(candidates, i + 1, arr_len, target - candidates[i])
            self.path.pop()
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func combinationSum2(candidates []int, target int) [][]int {
	arrLen := len(candidates)
	var results [][]int
	if arrLen == 0 {
		return results
	}

	var path []int
	sort.Ints(candidates)
	dfs(candidates, 0, arrLen, target, &results, path)
	return results
}

func dfs(candidates []int, begin, arrLen, target int, results *[][]int, path []int) {
	if target == 0 {
		*results = append(*results, append([]int{}, path...))
		return
	}

	for i := begin; i < arrLen; i++ {
		if target < candidates[i] {
			break
		}
		if i > begin && candidates[i] == candidates[i-1] {
			continue
		}

		path = append(path, candidates[i])
		dfs(candidates, i+1, arrLen, target-candidates[i], results, path)
		path = path[:len(path)-1]
	}
}

Posted on Edited on

题目(LeetCode #36)

判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

  • 数字 1-9 在每一行只能出现一次。
  • 数字 1-9 在每一列只能出现一次。
  • 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

下图是一个部分填充的有效的数独。

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例1：

输入：

1
2
3
4
5
6
7
8
9
10
11
[
    ["5","3",".",".","7",".",".",".","."],
    ["6",".",".","1","9","5",".",".","."],
    [".","9","8",".",".",".",".","6","."],
    ["8",".",".",".","6",".",".",".","3"],
    ["4",".",".","8",".","3",".",".","1"],
    ["7",".",".",".","2",".",".",".","6"],
    [".","6",".",".",".",".","2","8","."],
    [".",".",".","4","1","9",".",".","5"],
    [".",".",".",".","8",".",".","7","9"]
]

输出：

1
true

示例2：

输入：

1
2
3
4
5
6
7
8
9
10
11
[
    ["5","3",".",".","7",".",".",".","."],
    ["6",".",".","1","9","5",".",".","."],
    [".","9","8",".",".",".",".","6","."],
    ["8",".",".",".","6",".",".",".","3"],
    ["4",".",".","8",".","3",".",".","1"],
    ["7",".",".",".","2",".",".",".","6"],
    [".","6",".",".",".",".","2","8","."],
    [".",".",".","4","1","9",".",".","5"],
    [".",".",".",".","8",".",".","7","9"]
]

输出：

1
false

解释： 除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

说明：

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 给定数独序列只包含数字 1-9 和字符 ‘.’ 。
  • 给定数独永远是 9x9 形式的。

题解

参考题解

遍历 9 x 9 的数独，确保其满足：

  • 同一行中无重复数字
  • 同一列中无重复数字
  • 每个 3 x 3 的子数独中无重复数字

这三个条件可在一次迭代中完成，难点在于如何枚举子数独。

子数独的索引可通过 (row / 3) * 3 + column / 3 算得，其中 / 为整除（我也不知道别人是怎么想到的🙃）。

而判断是否有重复项可通过 Map 来判断，其中 key 为数字，value 为出现次数，在此使用二维数组来存储对应关系。

复杂度

由于单元格数量确定，始终为 81 个，故时间复杂度和空间复杂度均为 O(1) 。

实现

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean isValidSudoku(char[][] board) {
        int[][] rows = new int[9][9];
        int[][] columns = new int[9][9];
        int[][] boxes = new int[9][9];

        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char num = board[i][j];
                if (num == '.') continue;
                int n = num - '1';
                int box_index = (i / 3) * 3 + j / 3;

                rows[i][n] = rows[i][n] + 1;
                columns[j][n] = columns[j][n] + 1;
                boxes[box_index][n] = boxes[box_index][n] + 1;

                if (rows[i][n] > 1 || columns[j][n] > 1 || boxes[box_index][n] > 1)
                    return false;
            }
        }

        return true;
    }

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def isValidSudoku(self, board: list) -> bool:
        rows = [[0 for i in range(9)] for i in range(9)]
        columns = [[0 for i in range(9)] for i in range(9)]
        boxes = [[0 for i in range(9)] for i in range(9)]

        for i in range(9):
            for j in range(9):
                num = board[i][j]
                if num == '.': continue
                num = int(num) - 1
                box_index = (i // 3) * 3 + j // 3

                rows[i][num] += 1
                columns[j][num] += 1
                boxes[box_index][num] += 1

                if rows[i][num] > 1 or columns[j][num] > 1 or boxes[box_index][num] > 1:
                    return False

        return True

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func isValidSudoku(board [][]byte) bool {
    rows := [9][9]int{}
    columns := [9][9]int{}
    boxes := [9][9]int{}

    for i := 0; i < 9; i++ {
        for j := 0; j < 9; j++ {
            num := board[i][j]
            if num == '.' {
                continue
            }
            boxIndex := (i/3)*3 + j/3
            num = num - '1'
            rows[i][num]++
            columns[j][num]++
            boxes[boxIndex][num]++

            if rows[i][num] > 1 || columns[j][num] > 1 || boxes[boxIndex][num] > 1 {
                return false
            }
        }
    }

    return true
}

Posted on Edited on

题目(LeetCode #34)

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例1：

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

示例2：

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1, -1]

题解

方法一

先进行二分查找找到目标值 target ，再从两侧逐位逼近 mid ，判断是否与 target 相等即可找到开始合结束位置。

查找阶段时间复杂度为 O(logn) ，但在查找首尾时若输入数组全部为 target ，如 [8, 8, 8, 8 , 8] ，则将退化至 O(n) 。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[] searchRange(int[] nums, int target) {
        if (nums == null || nums.length == 0) return new int[]{-1, -1};
        int arrLen = nums.length;
        int left = 0, right = arrLen - 1;

        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] == target) {
                while (nums[left] != target) left++;
                while (nums[right] != target) right--;
                return new int[]{left, right};
            }
            
            if (nums[mid] < target) left = mid + 1;
            else right = mid - 1;
        }

        return new int[]{-1, -1};
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def searchRange(self, nums: list, target: int) -> list:
        if not nums or len(nums) == 0: return [-1, -1]
        arr_len = len(nums)
        left , right = 0, arr_len - 1

        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                while nums[left] != target: left += 1
                while nums[right] != target: right -= 1
                return [left, right]
            if nums[mid] < target: left = mid + 1
            else: right = mid - 1

        return [-1, -1]

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func searchRange(nums []int, target int) []int {
    arrLen := len(nums)
    if arrLen == 0 {
        return []int{-1, -1}
    }
    left, right := 0, arrLen - 1

    for left <= right {
        mid := (left + right) / 2
        if nums[mid] == target {
            for nums[left] != target {
                left++
            }
            for nums[right] != target {
                right--
            }
            return []int{left, right}
        }

        if nums[mid] < target {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }

    return []int{-1, -1}
}

方法二

在方法一的基础上，在查找首尾时也采用二分查找，时间复杂度整体为 O(logn) 。

与一般的二分法查找相等位置不同，查找起始位置的终止条件为：前一个元素与当前元素不相等；查找终止位置的结束条件为：后一个元素与当前元素不相等。

以输入 nums = [1, 2, 3, 3, 3, 3, 3, 3, 4] 和 target = 3 ，查找目标值的开始位置为例。

首先根据二分法找到与 target 相等的位置，在此即为 4 。

由于有 nums[mid] == nums[mid - 1] ，将 right 指向 mid - 1 。

重新计算 mid 为 3 // 2 = 1 。

此时有 nums[mid] < target ，将 left 指向 mid + 1 。

重新计算 mid 为 2，此时 nums[mid] != nums[mid - 1] ，返回 mid 当前值即为目标值的开始位置。

查找 target 的结束位置与上述过程类似，不再赘述。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int[] searchRange(int[] nums, int target) {
        return new int[] {
            binarySearch(nums, target, true),
            binarySearch(nums, target, false)
        };
    }

    public int binarySearch(int[] nums, int target, boolean isSearchFirst) {
        int arrLen = nums.length;
        if (arrLen == 0) return -1;

        int left = 0, right = arrLen - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] < target) left = mid + 1;
            else if (nums[mid] > target) right = mid - 1;
            else {
                if (isSearchFirst) {
                    if (mid > 0 && nums[mid] == nums[mid - 1]) right = mid - 1;
                    else return mid;
                } else {
                    if (mid < arrLen - 1 && nums[mid] == nums[mid + 1]) left = mid + 1;
                    else return mid;
                }
            }
        }

        return -1;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def searchRange(self, nums: list, target: int) -> list:
        if not nums or len(nums) == 0: return [-1, -1]
        return [
            self.binary_search(nums, target, True),
            self.binary_search(nums, target, False)
        ]

    def binary_search(self, nums: list, target: int, is_search_first: bool):
        arr_len = len(nums)
        left, right = 0, arr_len - 1
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] > target: right = mid - 1
            elif nums[mid] < target: left = mid + 1
            else:
                if is_search_first:
                    if mid > 0 and nums[mid] == nums[mid - 1]: right = mid - 1
                    else: return mid
                else:
                    if mid < arr_len - 1 and nums[mid] == nums[mid + 1]: left = mid + 1
                    else: return mid

        return -1

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
func searchRange(nums []int, target int) []int {
    return []int {
        binarySearch(nums, target, true),
        binarySearch(nums, target, false),
    }
}

func binarySearch(nums []int, target int, isSearchFirst bool) int {
    arrLen := len(nums)
    if arrLen == 0 {
        return -1
    }
    left, right := 0, arrLen - 1

    for left <= right {
        mid := (left + right) / 2
        if nums[mid] < target {
            left = mid + 1
        } else if nums[mid] > target {
            right = mid - 1
        } else {
            if isSearchFirst {
                if mid > 0 && nums[mid] == nums[mid - 1] {
                    right = mid -1
                } else {
                    return mid
                }
            } else {
                if mid < arrLen - 1 && nums[mid] == nums[mid + 1] {
                    left = mid + 1
                } else {
                    return mid
                }
            }
        }
    }

    return -1
}

Posted on Edited on

题目(LeetCode #31)

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。

1
2
3
1,2,3 -> 1,3,2
3,2,1 -> 1,2,3
1,1,5 -> 1,5,1

题解

参考题解

仿照 C++ 中 next_permutation 的实现方法。

分析

  1. 下一个数比当前数大：将后面的大数与前面的小数交换 ，如 123456 ，将 5 和 6 交换得到 123465 ；
  2. 下一个数的增幅应尽量小，使之满足字典序中的 下一个，为了满足该条件需进行如下操作：
    1. 在 尽可能靠右的低位进行交换，需从后向前查找；
    2. 将一个尽可能小的大数与前面的小数交换，如 123465 ，下一个排列应该将 5 与 4 交换而不是将 6 和 4 交换；
    3. 将大数换到前面后，需将大数后面的所有数重置为升序，升序排列即为最小排列。以 123465 为例：首先按照上一步，交换 5 和 4 ，得到 123564 。调整 5 后的数为升序，得到 123546 ，即为下一个排列。

实现步骤

  1. 从后向前查找第一个相邻升序的元素对 (i, j) ，满足 nums[i] < nums[j] 。此时 [j, end) 必然为降序；
  2. 在 [j, end) 从后向前查找第一个满足 nums[i] < nums[k] 的 k 。nums[i] 和 nums[k] 即为上述小数和大数；
  3. 交换 nums[i] 和 nums[k] ；
  4. 此时 [j, end) 必然为降序，逆置 [j, end) 使其升序；
  5. 若在步骤 1 找不到符合的相邻元素对，则说明当前数组单调递减，直接跳到步骤 4，整体逆序即可。

图解

以求 12385764 的下一个排列为例：

  1. 初始时：

  2. 从后向前查找第一个相邻升序的元素对 (i, j) ，这里 i=4 ，j=5 ，对应值为 5 和 7 ：

  3. 从后向前查找第一个大于 nums[i] 的值 nums[k] ，此例中 nums[i] = 5 ，故 nums[k]=6

  4. 交换 nums[i] 和 nums[k] ，即 5 和 6：

  5. 交换后 [j, end) 必仍是降序，逆置 [j, end) ，使其变为升序：

  6. 故 12385764 的下一个排列为 12386457 ，逆序后对比如下：

实现

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public void nextPermutation(int[] nums) {
        int arrLen = nums.length;
        if (arrLen <= 1) return;

        int i = arrLen - 2, j = arrLen - 1, k = arrLen - 1;

        while (i >= 0 && nums[i] >= nums[j]) {
            i--; j--;
        }

        if (i >= 0) {
            while (nums[i] >= nums[k]) k--;
            swap(i, k, nums);
        }

        for (i = j, j = arrLen - 1; i < j; i++, j--) {
            swap(i, j, nums);
        }
    }

    public void swap(int i, int j, int[] nums) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def nextPermutation(self, nums: list) -> None:
        arr_len = len(nums)
        if arr_len <= 1: return

        i, j, k = arr_len - 2, arr_len - 1, arr_len - 1

        while i >= 0 and nums[i] >= nums[j]:
            i -= 1
            j -= 1

        if i >= 0:
            while nums[i] >= nums[k]: k -= 1
            nums[i], nums[k] = nums[k], nums[i]

        i, j = j, arr_len - 1
        while i < j:
            nums[i], nums[j] = nums[j], nums[i]
            i += 1
            j -= 1

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func nextPermutation(nums []int)  {
    arrLen := len(nums)
    if arrLen <= 1 {
        return
    }

    i, j, k := arrLen - 2, arrLen - 1, arrLen - 1
    for i >= 0 && nums[i] >= nums[j] {
        i--
        j--
    }

    if i >= 0 {
        for nums[i] >= nums[k] {
            k--
        }
        nums[i], nums[k] = nums[k], nums[i]
    }

    i, j = j, arrLen - 1
    for i < j {
        nums[i], nums[j] = nums[j], nums[i]
        i++
        j--
    }
}

Posted on Edited on

题目(LeetCode #30)

给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。

注意子串要与 words 中的单词完全匹配，中间不能有其他字符，但不需要考虑 words 中单词串联的顺序。

示例 1：

输入：
  s = “barfoothefoobarman”,
  words = [“foo”,”bar”]
输出：[0,9]
解释：从索引 0 和 9 开始的子串分别是 “barfoo” 和 “foobar” 。输出的顺序不重要, [9,0] 也是有效答案。

示例 2：

输入：
  s = “wordgoodgoodgoodbestword”,
  words = [“word”,”good”,”best”,”word”]
输出：[]

题解

暴力解法

参考题解

创建两个 Map ，存储每个单词与单词出现次数的对应关系，wordMap 中保存输入数组 words 的词频信息；curMap 中保存逐位遍历输入字符串 s 的过程中产生的 wordMap 中含有的单词的词频。整体流程如下：

  • 创建 wordMap ，保存输入数组 words 中单词和对应的词频
  • 逐位遍历输入字符串 s ，记起始位为 start ，单词长度为 wordLen ，判断每次迭代 s[start, start + wordLen] 位置的单词是否在 wordMap 中
    • 若不存在，跳出当前循环
    • 若存在，则判断该词在 curMap 中出现次数是否超过其在 wordMap 中的词频
      • 若超过，则跳出当前循环
      • 若不超过，则增加 curMap 中该词的词频
  • 若从某位置 i 开始，遍历过程中所有的词都符合条件，则将 i 放入结果集中。

时间复杂度：假设 s 的长度是 n ，words 里有 m 个单词，那么时间复杂度为 O(n * m) 。

空间复杂度：两个 HashMap，假设 words 里有 m 个单词，就是 O(m) 。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import java.util.*;

class Solution {
    public List<Integer> findSubstring(String s, String[] words) {
        List<Integer> results = new ArrayList<>();
        int strLen = s.length();
        int arrLen = words.length;
        if (strLen == 0 || arrLen == 0) return results;
        int wordLen = words[0].length();

        HashMap<String, Integer> wordMap = new HashMap<>();
        for (String word : words) {
            int value = wordMap.getOrDefault(word, 0);
            wordMap.put(word, value + 1);
        }

        HashMap<String, Integer> curMap = new HashMap<>();
        int count = 0;
        for (int i = 0; i < strLen - arrLen * wordLen + 1; i++) {
            while (count < arrLen) {
                String curWord = s.substring(i + count * wordLen, i + (count + 1) * wordLen);
                if (wordMap.containsKey(curWord)) {
                    int value = curMap.getOrDefault(curWord, 0);
                    if (value + 1 > wordMap.get(curWord)) break;
                    curMap.put(curWord, value + 1);
                } else {
                    break;
                }
                count++;
            }
           	// 所有单词均符合条件
            if (count == arrLen) results.add(i);
            curMap.clear();
            count = 0;
        }

        return results;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def findSubstring(self, s: str, words: list) -> list:
        results = []
        s_len = len(s)
        arr_len = len(words)
        if s_len == 0 or arr_len == 0: return results
        word_len = len(words[0])

        word_map = {}
        for word in words:
            value = word_map.get(word)
            word_map[word] = value + 1 if value else 1

        for i in range(s_len - word_len * arr_len + 1):
            cur_map = {}
            count = 0
            while count < arr_len:
                cur_word = s[i + count * word_len: i + (count + 1) * word_len]
                if cur_word in word_map.keys():
                    value = cur_map.get(cur_word)
                    if value and value + 1 > word_map.get(cur_word): break
                    cur_map[cur_word] = value + 1 if value else 1
                else: break
                count += 1
            if count == arr_len: results.append(i)

        return results

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func findSubstring(s string, words []string) []int {
    var results []int
    sLen := len(s)
    arrLen := len(words)
    if sLen == 0 || arrLen == 0 {
        return results
    }
    wordLen := len(words[0])

    wordMap := make(map[string]int)
    for _, key := range words {
        wordMap[key] = wordMap[key] + 1
    }

    for i := 0; i < sLen - wordLen * arrLen + 1; i++ {
        curMap := make(map[string]int)
        count := 0
        for count < arrLen {
            curWord := s[i + wordLen * count: i + wordLen * (count + 1)]
            if wordMap[curWord] != 0 {
                curMap[curWord]++
                if curMap[curWord] > wordMap[curWord] {
                    break
                }
            } else {
                break
            }
            count++
        }
        if count == arrLen {
            results = append(results, i)
        }
    }
    return results
}

滑动窗口法

参考题解

使用滑动窗口来优化遍历过程，假定输入为字符串 s 和字符串数组 words 。取满足条件时的字符串长度为滑动窗口大小，即 windowSize = len(words) * len(words[0]) ，分别从 i=0,1,2 开始移动窗口，每次移动 len(words[0]) 的长度即可覆盖全部情况。跳过移动过程中的重复校验可降低时间复杂度，有以下三种重复情况：

  1. 匹配成功，窗口后移出现重复匹配

    1
    2
    s = 'barfoofoofoobarman'
    words = ['bar', 'foo', 'foo']

    上图中 s[3:9] 已在 i=0 为开头的窗口中校验过，确认存在于 words 数组中，且词频未越界，故无需重复判断，直接校验 i=9 之后的字符即可。

  2. 匹配失败，有 words 中不包含的单词

    1
    2
    s = 'barfoofoothefoobarman'
    words = ['bar', 'foo', 'foo']

    滑窗以 i=0 起始时，其中包含 words 数组中没有的 the ，匹配失败。而滑窗移动到 i=3 和 i=6 时又对 the 进行了重复校验，可直接将窗口移动到 i=9 位置跳过重复操作。

  3. 匹配失败，单词均在 words 中，但词频超出要求

    1
    2
    s = 'foobarbarfoobarman'
    words = ['bar', 'foo', 'foo']

    i=0 起始的窗口和 i=3 起始的窗口中均有两个 bar ，但 words 数组中仅有一个，可从 i=6 开始继续校验。

实际实现过程中，对窗口中的字符串进一步划分，每次只取 len(word[0]) 长度的子串，若该子串在 words 中且词频未越界，则增加该词在 curMap 中的词频。检验窗口中字符串的子串的过程中记录满足条件的单词数量 ，若当前窗口遍历完成后该数与 words 数组长度相等，则说明全部符合条件。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import java.util.*;

class Solution {
    public List<Integer> findSubstring(String s, String[] words) {
        List<Integer> results = new ArrayList<>();
        int sLen = s.length(), arrLen = words.length;
        if (sLen == 0 || arrLen == 0) return results;
        int wordLen = words[0].length();

        Map<String, Integer> wordMap = new HashMap<>();
        for (String word : words)
            wordMap.put(word, wordMap.getOrDefault(word, 0) + 1);

        Map<String, Integer> curMap = new HashMap<>();
        int windowSize = wordLen * arrLen;
        for (int i = 0; i < wordLen; i++) {
            int start = i;
            while (start + windowSize <= sLen) {
                String str = s.substring(start, start + windowSize);
                curMap.clear();
                int j = arrLen;
                while (j > 0) {
                    String curWord = str.substring((j - 1) * wordLen, j * wordLen);
                    int count = curMap.getOrDefault(curWord, 0) + 1;
                    if (count > wordMap.getOrDefault(curWord, 0)) break;
                    curMap.put(curWord, count);
                    j--;
                }
                if (j == 0) results.add(start);
                start += wordLen * Math.max(j, 1); // 若 j != 0 则说明匹配失败，窗口右移 j * wordLen，跳过已校验位置
            }
        }

        return results;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def findSubstring(self, s: str, words: list) -> list:
        results = []
        s_len, arr_len = len(s), len(words)
        if s_len == 0 or arr_len == 0: return results
        word_len = len(words[0])

        word_map = {}
        for word in words:
            word_map[word] = word_map.get(word, 0) + 1

        cur_map = {}
        window_size = word_len * arr_len
        for i in range(word_len):
            start = i
            while start + window_size <= s_len:
                cur_str = s[start: start + window_size]
                cur_map.clear()
                j = arr_len
                while j > 0:
                    word = cur_str[(j - 1) * word_len: j * word_len]
                    count = cur_map.get(word, 0) + 1
                    if count > word_map.get(word, 0): break
                    cur_map[word] = count
                    j -= 1
                if j == 0: results.append(start)
                start += word_len * max(j, 1)

        return results

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
func findSubstring(s string, words []string) []int {
    var results []int
    sLen, arrLen := len(s), len(words)
    if sLen == 0 || arrLen == 0 {
        return results
    }
    wordLen := len(words[0])

    wordMap := make(map[string]int)
    for _, word := range words {
        wordMap[word]++
    }

    windowSize := wordLen * arrLen;
    for i := 0; i < wordLen; i++ {
        start := i
        for start + windowSize <= sLen {
            curStr := s[start: start + windowSize]
            curMap := make(map[string]int)
            j := arrLen
            for j > 0 {
                curWord := curStr[(j-1) * wordLen: j * wordLen]
                count := curMap[curWord] + 1
                if count > wordMap[curWord] {
                    break
                }
                curMap[curWord] = count
                j--
            }
            if j == 0 {
                results = append(results, start)
            }
            start += wordLen * max(j, 1)
        }
    }

    return results
}

func max(a, b int) int {
    if a > b {
        return a
    } else {
        return b
    }
}

Posted on Edited on

堆的使用

Golang 中没有给出堆的具体实现，仅提供了标准容器库 container/heap ，需手动实现。

heap 接口定义如下

1
2
3
4
5
type Interface interface {
	sort.Interface
	Push(x interface{}) // add x as element Len()
	Pop() interface{}   // remove and return element Len() - 1.
}

该接口同时继承了 sort.Interface ，定义如下

1
2
3
4
5
6
7
8
9
type Interface interface {
	// Len is the number of elements in the collection.
	Len() int
	// Less reports whether the element with
	// index i should sort before the element with index j.
	Less(i, j int) bool
	// Swap swaps the elements with indexes i and j.
	Swap(i, j int)
}

故创建堆时需实现 Len() 、Less(i, j int) 、Swap(i, j int) 、Push(x interface{}) 、Pop() 五个方法。

向堆中插入节点时，堆会自动调整结构，Golang 中始终保持最后一个元素为堆顶，故 Pop 时返回最后一个节点并删除即可。

实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package main

import (
	"container/heap"
	"fmt"
	"math/rand"
	"strconv"
	"time"
)

type Person struct {
	Name string
	Age  int
}

type PersonHeap []Person

func (ph PersonHeap) Len() int {
	return len(ph)
}

func (ph PersonHeap) Swap(i, j int) {
	ph[i], ph[j] = ph[j], ph[i]
}

func (ph PersonHeap) Less(i, j int) bool {
	return ph[i].Age < ph[j].Age // 大根堆
}

func (ph *PersonHeap) Push(p interface{}) {
	*ph = append(*ph, p.(Person))
}

func (ph *PersonHeap) Pop() interface{} {
	n := len(*ph)
	result := (*ph)[n-1]
	*ph = (*ph)[:n-1]
	return result
}

func main() {
	rand.Seed(time.Now().Unix())
	hp := &PersonHeap{}
	for i := 0; i < 6; i++ {
		*hp = append(*hp, Person{"p" + strconv.Itoa(i), rand.Intn(50)})
	}
	fmt.Printf("原始切片: %#v\n", hp)

	heap.Init(hp)

	fmt.Printf("堆: %#v\n", hp)

	fmt.Println(hp.Pop())
	heap.Push(hp, Person{"newP", 30})

	fmt.Printf("%#v\n", hp)
}

例题(LeetCode #23)

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
package main

import (
	"container/heap"
	"fmt"
)

type ListNode struct {
	Val  int
	Next *ListNode
}

type PriorityQueue []*ListNode

func (pq PriorityQueue) Len() int {
	return len(pq)
}

func (pq PriorityQueue) Less(i, j int) bool {
	return pq[i].Val < pq[j].Val
}

func (pq *PriorityQueue) Swap(i, j int) {
	(*pq)[i].Val, (*pq)[j].Val = (*pq)[j].Val, (*pq)[i].Val
}

func (pq *PriorityQueue) Push(x interface{}) {
	*pq = append(*pq, x.(*ListNode))
}

func (pq *PriorityQueue) Pop() interface{} {
	result := (*pq)[len(*pq)-1]
	*pq = (*pq)[:len(*pq)-1]
	return result
}

func mergeKLists(lists []*ListNode) *ListNode {
	if lists == nil || len(lists) == 0 {
		return nil
	}

	dummyHead := &ListNode{0, nil}
	curNode := dummyHead
	var pq PriorityQueue

	for _, list := range lists {
		tmp := list
		for tmp != nil {
			heap.Push(&pq, tmp)
			tmp = tmp.Next
		}
	}

	for len(pq) != 0 {
		curNode.Next = heap.Pop(&pq).(*ListNode)
		curNode = curNode.Next
	}
	curNode.Next = nil

	return dummyHead.Next
}

func main() {
	l1 := &ListNode{1, nil}
	l1.Next = &ListNode{4, nil}
	l1.Next.Next = &ListNode{5, nil}

	l2 := &ListNode{1, nil}
	l2.Next = &ListNode{3, nil}
	l2.Next.Next = &ListNode{4, nil}

	l3 := &ListNode{2, nil}
	l3.Next = &ListNode{6, nil}

	lists := []*ListNode{l1, l2, l3}

	result := mergeKLists(lists)
	for result != nil {
		fmt.Printf("%d ", result.Val)
		result = result.Next
	}
}

Posted on Edited on

题目(LeetCode #19)

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：

给定的 n 保证是有效的。

进阶：

你能尝试使用一趟扫描实现吗？

题解

递归法

利用递归的特性，从递归栈底向上累加即为倒数索引。

removeNode 最终返回的值为输入链表的长度，若该返回值与 n 相等，则说明去掉的是第一个节点，此时头节点为 head.next 。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class ListNode {
    int val;
    ListNode next;
    ListNode(int x) {
        val = x;
    }
}

public class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
    	return removeNode(head, n) == n ? head.next : head; 
    }

    public int removeNode(ListNode node, int n) {
        if (node.next == null) return 1;
        int m = removeNode(node.next, n);
        if (m == n)
            node.next = node.next.next;

        return m + 1;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        return head.next if self.remove_node(head, n) == n else head

    def remove_node(self, head: ListNode, n: int) -> int:
        if not head.next: return 1
        m = self.remove_node(head.next, n)
        if m == n:
            head.next = head.next.next

        return m + 1

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
package main

type ListNode struct {
    Val  int
    Next *ListNode
}

func removeNthFromEnd(head *ListNode, n int) *ListNode {
    if removeNode(head, n) == n {
        return head.Next
    } else {
        return head
    }
}

func removeNode(head *ListNode, n int) int {
    if head.Next == nil {
        return 1
    }

    m := removeNode(head.Next, n)
    if m == n {
        head.Next = head.Next.Next
    }

    return m + 1
}

双指针法

使用快慢指针来查找索引，快指针先移动 n 个位置，再同时移动两指针，当快指针指向链表的尾节点时，慢指针所指即为倒数第 n 个节点。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        if (head == null || head.next == null) return null;

        ListNode fast = head, slow = head;
        for (int i = 0; i < n; i++)
            fast = fast.next;

        if (fast == null)
            return head.next;

        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }

        slow.next = slow.next.next;
        return head;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        fast, slow = head, head
        for i in range(n):
            fast = fast.next

        if not fast: return head.next

        while fast.next:
            fast = fast.next
            slow = slow.next

        slow.next = slow.next.next

        return head

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func removeNthFromEnd(head *ListNode, n int) *ListNode {
    fast, slow := head, head

    for i := 0; i < n; i++ {
        fast = fast.Next
    }

    if fast == nil {
        return head.Next
    }

    for fast.Next != nil {
        fast = fast.Next
        slow = slow.Next
    }
    slow.Next = slow.Next.Next

    return head
}

Posted on Edited on

题目(LeetCode #16)

给定一个包括 n 个整数的数组 nums 和 一个目标值 target 。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

示例：

输入： nums = [-1,2,1,-4], target = 1

输出： 2

解释： 与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

提示：

  • 3 <= nums.length <= 10³
  • -10³ <= nums[i] <= 10³
  • -104> <= target <= 104

题解

本题与三数之和类似 ，可采用双指针法，差别在于本题可以有重复元素。

由于处理过程中数组已经过排序，故在遍历数组元素的过程中，若 nums[i] + nums[L] + nums[R] > target ，需将 R 左移，以减小三数和，进而减小其与 target 的差值；若 nums[i] + nums[L] + nums[R] < target ，需将 L 右移，增大三数和来达到相同目的。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.Arrays;

public class Solution {
    public int threeSumClosest(int[] nums, int target) {
        int n = nums.length;
        if (n == 3) return nums[0] + nums[1] + nums[2];

        Arrays.sort(nums);
        int result = 0;
        int minDiff = Integer.MAX_VALUE;


        for (int i = 0; i < n - 2; i++) {
            int l = i + 1, r = n - 1;

            while (l < r) {
                int curSum = nums[i] + nums[l] + nums[r];

                if (curSum == target) return curSum;
                else if (curSum > target) r--;
                else l++;

                int curDiff = Math.abs(curSum - target);
                if (curDiff < minDiff) {
                    minDiff = curDiff;
                    result = curSum;
                }
            }
        }

        return result;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def threeSumClosest(self, nums: list, target: int) -> int:
        list_len = len(nums)
        if not nums or list_len < 3: return 0

        nums.sort()
        min_diff = float('inf')
        result = 0

        for i in range(list_len):
            l = i + 1
            r = list_len - 1
            while l < r:
                cur_sum = nums[i] + nums[l] + nums[r]
                if cur_sum == target: return cur_sum
                cur_diff = abs(cur_sum - target)
                if cur_diff < min_diff:
                    result = cur_sum
                    min_diff = cur_diff

                if cur_sum > target: r -= 1
                else: l += 1

        return result

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
package main

import (
    "math"
    "sort"
)

func threeSumClosest(nums []int, target int) int {
    arrLen := len(nums)
    if nums == nil || arrLen < 3 {
        return 0
    }

    sort.Ints(nums)
    result, curSum, curDiff := 0, 0, 0
    minDiff := math.MaxInt32

    for i, v := range nums {
        L, R := i+1, arrLen-1
        for L < R {
            curSum = v + nums[L] + nums[R]
            if curSum == target {
                return curSum
            }
            curDiff = int(math.Abs(float64(curSum - target)))
            if curDiff < minDiff {
                result = curSum
                minDiff = curDiff
            }

            if curSum > target {
                R--
            } else {
                L++
            }
        }
    }

    return result
}

Posted on Edited on

题目(LeetCode #15)

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
 [-1, 0, 1],
 [-1, -1, 2]
]

题解

双指针法

若要找出所有满足条件的解，需三个变量 a , b , c 的所有情况且不能重复，若直接遍历时间复杂度为 O(N³) ，本题的关键在于如何降低时间复杂度和去除重复解。

可采用双指针法来实现遍历的不重不漏，首先将数组进行排序，再使L 指向 i+1 ，R 指向末尾元素，两指针向中间移动直至相遇为止。在遍历过程中

  • 若 nums[i] 与 nums[i-1] 、nums[L] 与 nums[L+1] 、nums[R] 与 nums[R-1] 相等即说明遇到了重复元素，跳过即可；
  • 若 nums[i] + nums[L] + nums[R] == target ，即为一组解，L 和 R 同时移动；
  • 若 nums[i] + nums[L] + nums[R] > target ，R 应向左移动以减小三数之和；
  • 若 nums[i] + nums[L] + nums[R] < target ，L 应向右移动以增大三数之和。

时间复杂度

  • 时间复杂度：O(N²) ，数组排序 O(NlogN) ，遍历数组 O(N) ，双指针遍历 O(N) ，总体为 O(NlogN) + O(N) * O(N) ，O(N²)
  • 空间复杂度：O(1)

参考题解：LeetCode

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import java.util.List;
import java.util.ArrayList;
import java.util.Arrays;

public class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int listLen = nums.length;
        List<List<Integer>> results = new ArrayList<>();
        if (listLen < 3) return results;

        Arrays.sort(nums);
        int L, R;

        for (int i = 0; i < listLen; i++) {
            if (nums[i] > 0) return results;
            if (i > 0 && nums[i] == nums[i - 1]) continue;
            L = i + 1;
            R = listLen - 1;
            while (L < R) {
                if (nums[i] + nums[L] + nums[R] == 0) {
                    results.add(new ArrayList<>(Arrays.asList(nums[i], nums[L], nums[R])));
                    while (L < R && nums[L] == nums[L + 1]) L++;
                    while (L < R && nums[R] == nums[R - 1]) R--;
                    L++; R--;
                } else if (nums[i] + nums[L] + nums[R] > 0) {
                    R--;
                } else {
                    L++;
                }
            }
        }

        return results;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def threeSum(self, nums: list) -> list:
        list_len = len(nums)
        results = []
        if not nums or list_len < 3: return results

        nums.sort()
        for i in range(list_len):
            if nums[i] > 0: return results
            if (i > 0 and nums[i] == nums[i - 1]): continue
            L = i + 1
            R = list_len - 1
            while L < R:
                if nums[i] + nums[L] + nums[R] == 0:
                    results.append([nums[i], nums[L], nums[R]])
                    while L < R and nums[L] == nums[L + 1]: L += 1
                    while L < R and nums[R] == nums[R - 1]: R -= 1
                    L += 1
                    R -= 1
                elif nums[i] + nums[L] + nums[R] > 0:
                    R -= 1
                else:
                    L += 1
        return results

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package main

import (
    "sort"
)

func threeSum(nums []int) [][]int {
    arrLen := len(nums)
	var results [][]int
	if nums == nil || arrLen < 3 {
		return results
	}

	sort.Ints(nums)

	for i := 0; i < arrLen; i++ {
		if nums[i] > 0 {
			return results
		}

		if i > 0 && nums[i] == nums[i-1] {
			continue
		}

		L, R := i+1, arrLen-1
		for L < R {
			if nums[i]+nums[L]+nums[R] == 0 {
				results = append(results, []int{nums[i], nums[L], nums[R]})
				for L < R && nums[L] == nums[L+1] {
					L++
				}
				for L < R && nums[R] == nums[R-1] {
					R--
				}
				L++
				R--
			} else if nums[i]+nums[L]+nums[R] > 0 {
				R--
			} else {
				L++
			}
		}
	}

	return results
}