Leaky Cauldron
0%

二叉搜索树中的中序后继

Posted on Edited on

LeetCode #285

二叉搜索树中的中序后继

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

节点 p 的后继是值比 p.val 大的节点中键值最小的节点。

示例 1：

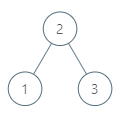
输入：root = [2,1,3], p = 1
输出：2
解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。

示例 2：

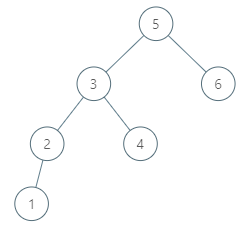
输入：root = [5,3,6,2,4,null,null,1], p = 6
输出：null
解释：因为给出的节点没有中序后继，所以答案就返回 null 了。

提示：

  • 树中节点的数目在范围 [1, 104] 内。
  • -10^5 <= Node.val <= 10^5
  • 树中各节点的值均保证唯一。

题解

利用二叉搜索树中序遍历单调递增求解：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    private TreeNode result = null;

    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        if (root == null || result != null) return result;
        inorderSuccessor(root.left, p);
        if (root.val > p.val && result == null) result = root;
        inorderSuccessor(root.right, p);

        return result;
    }
}

LeetCode #510

二叉搜索树中的中序后继 II

给定一棵二叉搜索树和其中的一个节点 node ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

一个节点 node 的中序后继是键值比 node.val 大所有的节点中键值最小的那个。

你可以直接访问结点，但无法直接访问树。每个节点都会有其父节点的引用。节点 Node 定义如下：

1
2
3
4
5
6
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

示例 1：

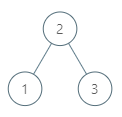
输入：tree = [2,1,3], node = 1
输出：2
解析：1 的中序后继结点是 2 。注意节点和返回值都是 Node 类型的。

示例 2：

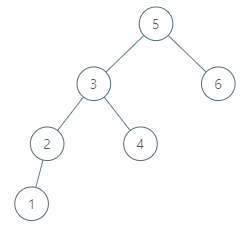
输入：tree = [5,3,6,2,4,null,null,1], node = 6
输出：null
解析：该结点没有中序后继，因此返回 null 。

示例 3：

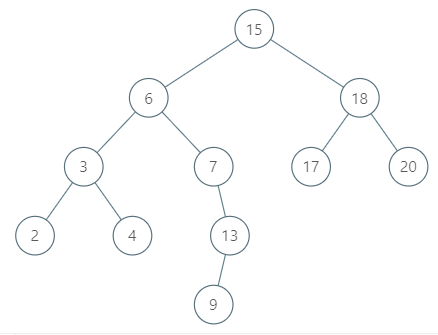
输入：tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15
输出：17

示例 4：

输入：tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13
输出：15

示例 5：

输入：tree = [0], node = 0
输出：null

提示：

  • 树中节点的数目在范围 [1, 104] 内。
  • -10^5 <= Node.val <= 10^5
  • 树中各结点的值均保证唯一。

题解

二叉搜索树中的任意节点的中序后继可能有两种情况：

  • 如果该节点有右子树，则后继在右孩子节点的左子树的最低点

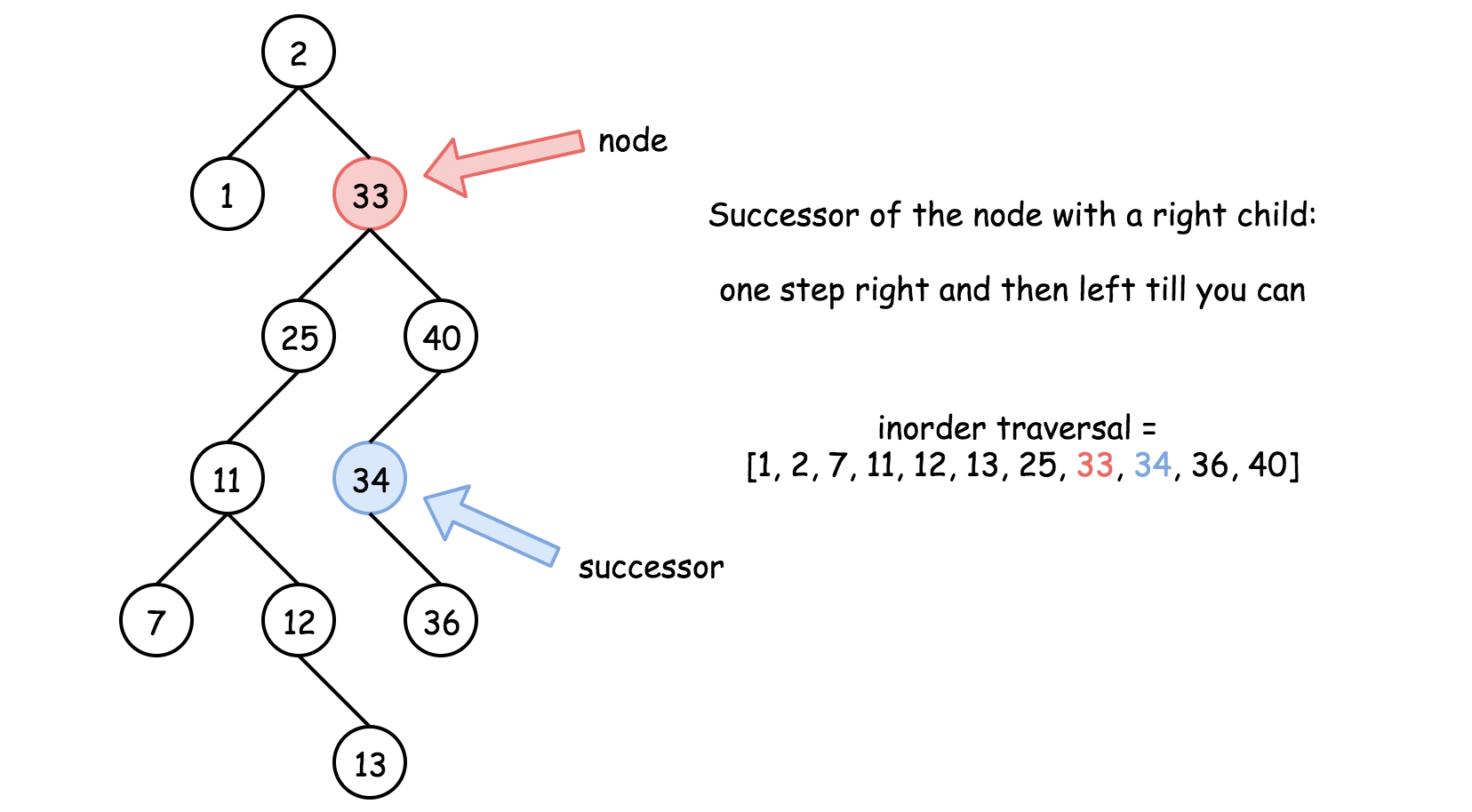
  • 如果该节点没有右子树，则后继在相对该节点树中较高的地方，向上找直到某个节点 node，node 在其父节点的左子树上为止

1
2
3
4
5
6
7
8
9
10
11
12
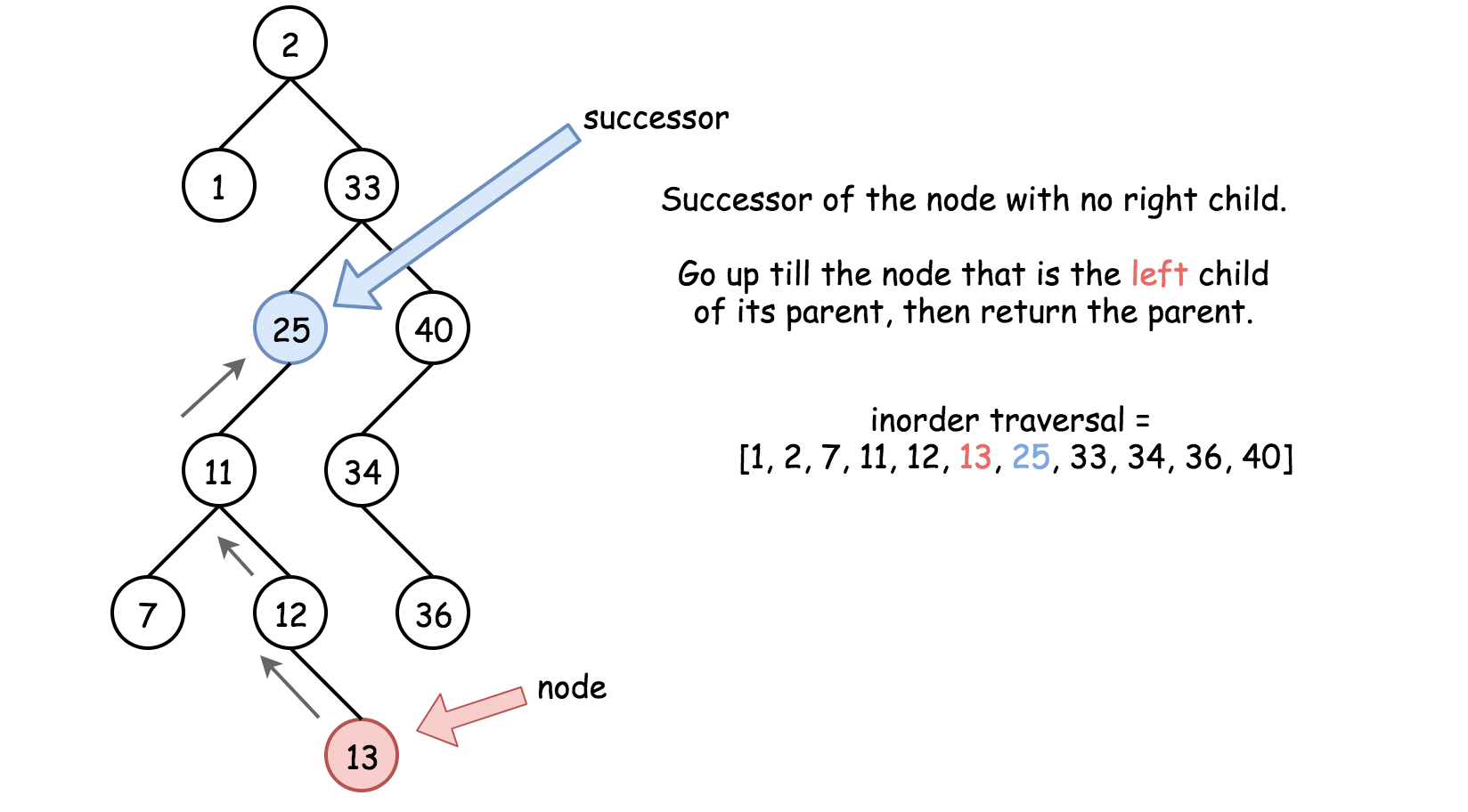
13
class Solution {
    public Node inorderSuccessor(Node node) {
        if (node.right != null) {
            node = node.right;
            while (node.left != null) node = node.left;
            return node;
        }

        /* 只要 node 在其父节点的右子树上就一直往上找 */
        while (node.parent != null && node.parent.right == node) node = node.parent;
        return node.parent;
    }
}