二叉树中所有距离为 K 的结点

题目

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 k 。

返回到目标结点 target 距离为 k 的所有结点的值的列表。 答案可以以 任何顺序 返回。

示例 1：

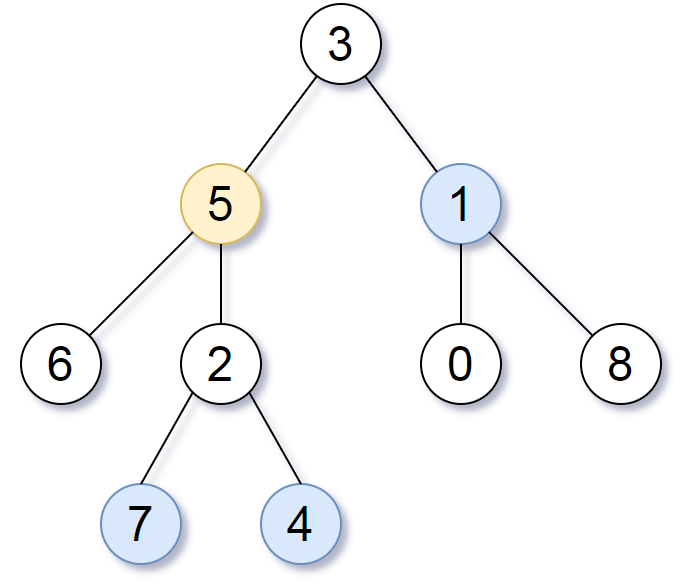
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
输出：[7,4,1]
解释：所求结点为与目标结点（值为 5）距离为 2 的结点，值分别为 7，4，以及 1

示例 2：

输入: root = [1], target = 1, k = 3
输出: []

提示:

• 节点数在 [1, 500] 范围内
• 0 <= Node.val <= 500
• Node.val 中所有值 不同
• 目标结点 target 是树上的结点。
• 0 <= k <= 1000

链式前向星

本题的难点在于建图，用以保存相邻节点之间的关系。树实际上也是无向图，在此可引入链式前向星的方法，用数组保存保存图中节点的关系。

一个简单的链式前向星实现主要包含以下元素：

• idx：对图中的边进行编号；
• heads 数组：保存图中的所有节点；
• edges 数组：保存图中每条边的权重；
• ends 数组：保存每条边的终点索引；
• nexts 数组：保存下一条边的索引。

代码模板如下（参考: @Scarb）：

int N; // 最大节点数量
int M; // 最大边数

int idx = 0;				// 边索引
int[] heads = new int[N];	// heads[a] 表示以 a 节点为起点的最新一条边的索引
int[] edges = new int[M];	// edges[idx] 表示索引为 idx 的边的权重
int[] ends = new int[M];	// ends[idx] 表示索引为 idx 的边的终点节点在 heads 中的索引
int[] nexts = new int[M];	// nexts[idx] 表示索引为 idx 的边的下一条同起点的边的索引，用于找到同起点的下一条边

Arrays.fill(heads, -1);		// 设置所有节点都没有边

// 添加一条起点为 a，终点为 b，权重为 w 的边，边的索引为 idx，采用了类似尾插法的方法
public void add(int a, int b, int w) {
    ends[idx] = b;
    edges[idx] = w;
    nexts[idx] = a;
    heads[a] = idx++;
}

// 遍历从 a 出发的所有的边
// 从head[a]取出a节点最新一条边的索引idx，开始遍历。
// 每次通过next[idx]获取以该节点为起点的下一条边的索引
// 直到下一条边的索引为-1，即没有下一条边
for (int idx = head[a]; idx != -1; idx = nexts[idx]) {
    int end = ends[idx];
    int w = edges[idx];
}

题解

链式前向星 + DFS

class Solution {
    private int N = 501, M = N * 4, idx = 0;
    private int[] head = new int[N], end = new int[M], next = new int[M];
    private boolean[] visited = new boolean[N];
    private List<Integer> result;

    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        Arrays.fill(head, -1);
        dfs(root);

        visited[target.val] = true;

        result = new ArrayList<>();
        find(target.val, k);

        return result;
    }

    private void add(int a, int b) {
        end[idx] = b;
        next[idx] = head[a];
        head[a] = idx++;
    }

    private void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }

    private void find(int root, int k) {
        if (k == 0) {
            result.add(root);
            return;
        }

        for (int h = head[root]; h != -1; h = next[h]) {
            int e = end[h];
            if (!visited[e]) {
                visited[e] = true;
                find(e, k - 1);
            }
        }
    }
}

链式前向星 + BFS

class Solution {

    private int N = 501, M = N * 4, idx = 0;
    private int[] heads = new int[N], ends = new int[M], nexts = new int[M];
    private boolean[] visited = new boolean[N];

    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        List<Integer> result = new ArrayList<>();
        Arrays.fill(heads, -1);
        dfs(root);

        Queue<Integer> queue = new ArrayDeque<>();
        queue.add(target.val);
        visited[target.val] = true;

        while (!queue.isEmpty() && k >= 0) {
            for (int i = queue.size(); i > 0; i--) {
                int cur = queue.poll();
                if (k == 0) {
                    result.add(cur);
                    continue;
                }

                for (int h = heads[cur]; h != -1; h = nexts[h]) {
                    int e = ends[h];
                    if (!visited[e]) {
                        queue.add(e);
                        visited[e] = true;
                    }
                }
            }
            k--;
        }

        return result;
    }

    private void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }

    private void add(int a, int b) {
        ends[idx] = b;
        nexts[idx] = heads[a];
        heads[a] = idx++;
    }
}

保存父节点 + DFS

class Solution {
    private Map<TreeNode, TreeNode> parentMap;
    private Set<TreeNode> visited;
    private List<Integer> result;

    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        parentMap = new HashMap<>();
        dfs(root);

        visited = new HashSet<>();
        visited.add(target);

        result = new ArrayList<>();
        find(target, k);

        return result;
    }

    private void find(TreeNode root, int k) {
        if (k == 0) {
            result.add(root.val);
            return;
        }

        if (root.left != null && !visited.contains(root.left)) {
            visited.add(root.left);
            find(root.left, k - 1);
        }

        if (root.right != null && !visited.contains(root.right)) {
            visited.add(root.right);
            find(root.right, k - 1);
        }

        TreeNode parent = parentMap.get(root);
        if (parent != null && !visited.contains(parent)) {
            visited.add(parent);
            find(parent, k - 1);
        }
    }

    private void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            parentMap.put(root.left, root);
            dfs(root.left);
        }
        if (root.right != null) {
            parentMap.put(root.right, root);
            dfs(root.right);
        }
    }
}