Leaky Cauldron
0%

无向图中连通分量的数目

Posted on Edited on

题目(LeetCode #323)

你有一个包含 n 个节点的图。给定一个整数 n 和一个数组 edges ，其中 edges[i] = [ai, bi] 表示图中 ai 和 bi 之间有一条边。

返回 图中已连接分量的数目 。

示例1：

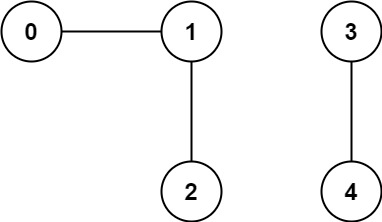
输入: n = 5, edges = [[0, 1], [1, 2], [3, 4]]
输出: 2

示例2：

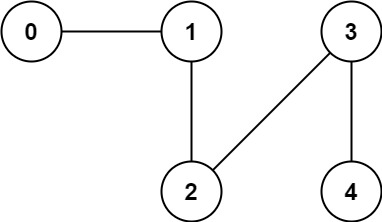
输入: n = 5, edges = [[0,1], [1,2], [2,3], [3,4]]
输出: 1

提示：

  • 1 <= n <= 2000
  • 1 <= edges.length <= 5000
  • edges[i].length == 2
  • 0 <= ai <= bi < n
  • ai != bi
  • edges 中不会出现重复的边

题解

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int countComponents(int n, int[][] edges) {
        if (n == 0 || edges == null) return 0;

        List<List<Integer>> adjList = new ArrayList<>();
        for (int i = 0; i < n; i++) adjList.add(new ArrayList<>());
        for (int[] edge : edges) {
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }

        int count = 0;
        boolean[] visited = new boolean[n];
        for (int i = 0; i < n; i++) {
            if (visited[i]) continue;

            count++;
            Deque<Integer> queue = new ArrayDeque<>();
            queue.add(i);
            while (!queue.isEmpty()) {
                int cur = queue.poll();
                visited[cur] = true;
                for (int next : adjList.get(cur)) {
                    if (!visited[next]) queue.add(next);
                }
            }
        }


        return count;
    }
}

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    private int n;
    private boolean[] visited;
    List<List<Integer>> adjList;

    public int countComponents(int n, int[][] edges) {
        if (n == 0 || edges == null) return 0;

        this.n = n;
        adjList = new ArrayList<>();
        visited = new boolean[n];
        for (int i = 0; i < n; i++) adjList.add(new ArrayList<>());
        for (int[] edge : edges) {
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }

        int count = 0;
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                dfs(i);
            	count++;
            }
        }

        return count;
    }

    public void dfs(int i) {
        if (visited[i]) return;

        visited[i] = true;
        for (int next : adjList.get(i)) dfs(next);
    }
}

并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class UnionFind {
    private int[] parents, rank;
    int unionCnt = 0;

    public UnionFind(int[] parents) {
        this.parents = parents;
        this.rank = new int[parents.length];
        Arrays.fill(this.rank, 1);
    }

    public int find(int x) {
        if (parents[x] == x) return x;
        return parents[x] = find(parents[x]);
    }

    public void union(int x, int y) {
        int xRoot = find(x), yRoot = find(y);

        if (xRoot == yRoot) return;

        unionCnt++;
        if (rank[yRoot] <= rank[xRoot]) parents[yRoot] = xRoot;
        else parents[xRoot] = yRoot;
        if (rank[xRoot] == rank[yRoot]) rank[xRoot]++;
    }
}

class Solution {
    public int countComponents(int n, int[][] edges) {
        if (n == 0 || edges == null) return 0;

        int[] parents = new int[n];
        for (int i = 0; i < n; i++) parents[i] = i;
        UnionFind uf = new UnionFind(parents);

        for (int[] edge : edges) uf.union(edge[0], edge[1]);

        return n - uf.unionCnt;
    }
}