题目(LeetCode #490)
由空地(用 0 表示)和墙(用 1 表示)组成的迷宫 maze 中有一个球。球可以途经空地向 上、下、左、右 四个方向滚动,且在遇到墙壁前不会停止滚动。当球停下时,可以选择向下一个方向滚动。
给你一个大小为 m x n 的迷宫 maze ,以及球的初始位置 start 和目的地 destination ,其中 start = [startrow, startcol] 且 destination = [destinationrow, destinationcol] 。请你判断球能否在目的地停下:如果可以,返回 true ;否则,返回 false 。
你可以 假定迷宫的边缘都是墙壁(参考示例)。
示例1:
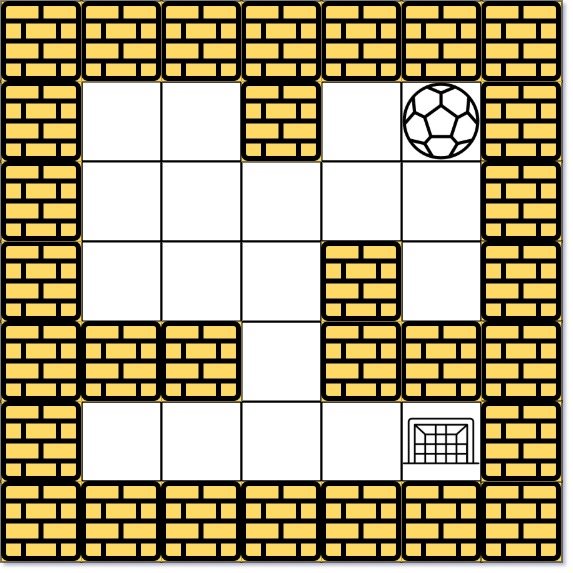
输入:maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
输出:true
解释:一种可能的路径是 : 左 -> 下 -> 左 -> 下 -> 右 -> 下 -> 右。
示例2:
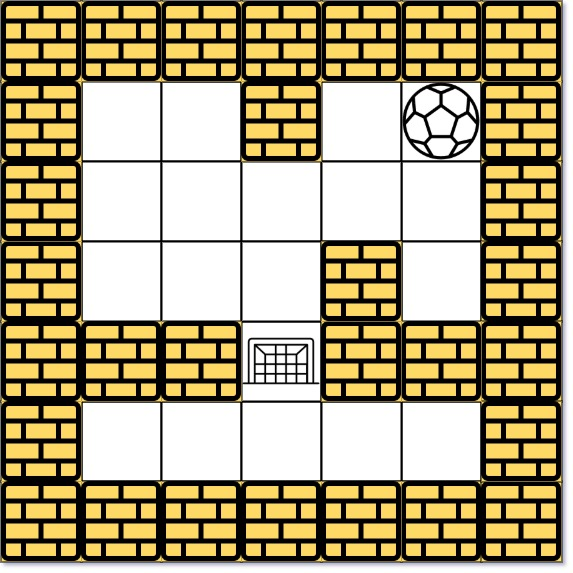
输入:maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
输出:false
解释:不存在能够使球停在目的地的路径。注意,球可以经过目的地,但无法在那里停驻。
示例3:
输入:maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1]
输出:false
提示:
m == maze.lengthn == maze[i].length1 <= m, n <= 100maze[i][j] is 0 or 1start.length == 2destination.length == 2- 0 <= startrow, destinationrow <= m
- 0 <= startcol, destinationcol <= n
- 球和目的地都在空地上,且初始时它们不在同一位置
- 迷宫 至少包括 2 块空地
题解
本题可采用 BFS 或 DFS 求解,与岛屿问题不同的是,小球只有在碰到墙壁时才能停止并更改方向。
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
if (maze == null || maze.length == 0 || maze[0].length == 0) return false;
int m = maze.length, n = maze[0].length;
Deque<int[]> queue = new ArrayDeque<>();
queue.add(start);
while (!queue.isEmpty()) {
int[] cur = queue.poll();
int i = cur[0], j = cur[1];
if (maze[i][j] == 2) continue;
if (i == destination[0] && j == destination[1]) return true;
maze[i][j] = 2;
int l = j - 1, r = j + 1, u = i - 1, d = i + 1;
while (l >= 0 && maze[i][l] != 1) l--;
if (maze[i][l + 1] != 2) queue.add(new int[]{i, l + 1});
while (r < n && maze[i][r] != 1) r++;
if (maze[i][r - 1] != 2) queue.add(new int[]{i, r - 1});
while (u >= 0 && maze[u][j] != 1) u--;
if (maze[u + 1][j] != 2) queue.add(new int[]{u + 1, j});
while (d < m && maze[d][j] != 1) d++;
if (maze[d - 1][j] != 2) queue.add(new int[]{d - 1, j});
}
return false;
}
}
|
DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
int[][] maze;
int[] destination;
int m, n;
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
if (maze == null || maze.length == 0 || maze[0].length == 0) return false;
this.maze = maze;
this.destination = destination;
m = maze.length;
n = maze[0].length;
return dfs(start[0], start[1]);
}
private boolean dfs(int i, int j) {
if (i < 0 || i >= m || j < 0 || j >= n || maze[i][j] != 0) return false;
if (i == destination[0] && j == destination[1]) return true;
maze[i][j] = 2;
int l = j - 1, r = j + 1, u = i - 1, d = i + 1;
while (l >= 0 && maze[i][l] != 1) l--;
if (dfs(i, l + 1)) return true;
while (r < n && maze[i][r] != 1) r++;
if (dfs(i, r - 1)) return true;
while (u >= 0 && maze[u][j] != 1) u--;
if (dfs(u + 1, j)) return true;
while (d < m && maze[d][j] != 1) d++;
if (dfs(d - 1, j)) return true;
return false;
}
}
|

