Leaky Cauldron
0%

Maximum Average Subarray II

Posted on Edited on

题目(LeetCode #644)

Given an array consisting of n integers, find the contiguous subarray whose length is greater than or equal to k that has the maximum average value. And you need to output the maximum average value.

Input: [1, 12, -5, -6, 50, 3], k = 4
Output: 12.75
Explanation:
when length is 5, maximum average value is 10.8,
when length is 6, maximum average value is 9.16667.
Thus return 12.75.

Note:

  1. 1 <= k <= n <= 10,000.
  2. Elements of the given array will be in range [-10,000, 10,000].
  3. The answer with the calculation error less than 10-5 will be accepted.

题解

本题的技巧性较强，可采用滑动窗口加二分法求解，用猜平均值的方式逼近真实值，实现的关键在于找到二分的条件。对于一个数组来说，其所有可能的子数组的最大平均值必介于最大值和最小值之间。取 mid = (min + max) / 2.0，对数组依次求长度大于等于 k 的所有可能的子数组的平均值。若平均值序列中有值大于等于 mid，则最大平均值必位于 [mid, max] 区间（即 l = mid）；若平均值序列中所有值都小于 mid，则最大平均值必位于 [min, mid] 上（即 r = mid）。其中，在计算平均值时，可将计算简化为 xi - mid 的和与 0 进行比较。

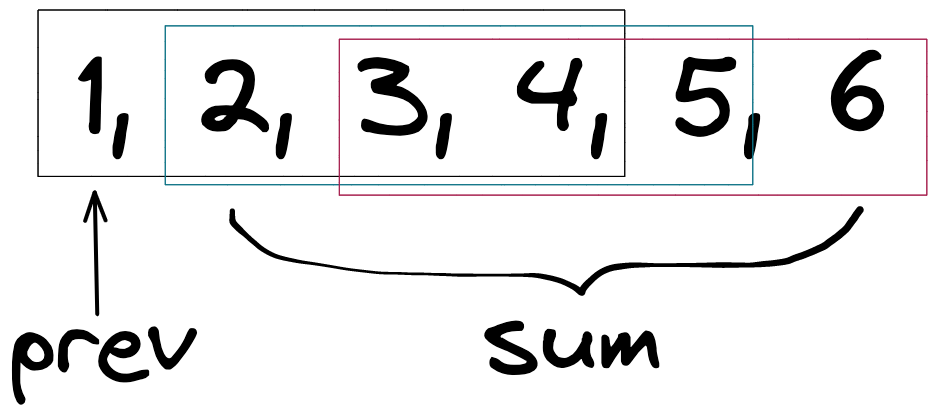
另一个 trick 是在计算数组所有可能的平均值时，不必对所有长度大于 k 的子数组再次进行遍历，只需在前 k 个元素和的基础上向右扩增，再减去前几项的和既可得到新的子数组的和。如 k = 4，当滑动窗口中包含 0 ~ 5 六个元素时，如果想得到长度为 5 和 4 的子数组的和，只需分别减去第 0 和第 0 ~ 1 个元素即可。而由于是在 mid 两侧判断是否存在子数组满足条件，故直接比较子数组的最大和与最小的前缀和的大小既可。

参考视频：【LeetCode 刷题讲解】644. Maximum Average Subarray II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
        for (int num : nums) {
            min = Math.min(min, num);
            max = Math.max(max, num);
        }

        double l = min, r = max;
        while (r - l > 0.00001) {
            double mid = (l + r) / 2.0;
            if (exist(nums, k, mid)) l = mid;
            else r = mid;
        }

        return l;
    }

    private boolean exist(int[] nums, int k, double mid) {
        double sum = 0, prev = 0, minPrev = 0;
        for (int i = 0; i < k; i++) sum += nums[i] - mid;
        if (sum >= 0) return true;

        for (int i = k; i < nums.length; i++) {
            sum += nums[i] - mid;
            prev += nums[i - k] - mid;
            minPrev = Math.min(prev, minPrev);  // 比较 子数组的最大和 与 最小的前缀和 的大小
            if (sum - minPrev >= 0) return true;
        }

        return false;
    }
}