给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1, 2, 3]
输出:
[
[1, 2, 3],
[1, 3, 2],
[2, 1, 3],
[2, 3, 1],
[3, 1, 2],
[3, 2, 1]
]
题解
使用 visited 数组标记已访问过的元素。
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| import java.util.*;
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
dfs(results, nums, new ArrayList<>(), new int[nums.length]);
return results;
}
public void dfs(List<List<Integer>> results, int[] nums, ArrayList<Integer> tmp, int[] visited) {
if (tmp.size() == nums.length) {
results.add(new ArrayList<>(tmp));
return;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i] == 1) continue;
tmp.add(nums[i]);
visited[i] = 1;
dfs(results, nums, tmp, visited);
visited[i] = 0;
tmp.remove(tmp.size() - 1);
}
}
}
|
Python
使用切片和 list 的加法,在向下递归时略过当前元素即实现了对访问过元素的标记。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution:
def permute(self, nums: list) -> list:
results = []
def dfs(nums, tmp):
if not nums:
results.append(tmp)
return
for i in range(len(nums)):
dfs(nums[:i] + nums[i + 1:], tmp + [nums[i]])
dfs(nums, [])
return results
def permute1(self, nums: list) -> list:
return list(itertools.permutations(nums))
|
调用 Python 的内置函数实现如下
1
2
3
4
5
| import itertools
class Solution:
def permute(self, nums: list) -> list:
return list(itertools.permutations(nums))
|
Go
Go 在实现时需注意 append(nums, 2) 不会修改 nums 数组存储的内容,但 append(nums[:i], 2) 会使 nums 数组发生改变。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| package main
import "fmt"
func permute(nums []int) [][]int {
var results [][]int
dfs(&results, nums, []int{})
return results
}
func dfs(results *[][]int, nums, tmp []int) {
if len(nums) == 0 {
*results = append(*results, append([]int{}, tmp...))
return
}
for i := 0; i < len(nums); i++ {
dfs(results, combinedArr(nums[:i], nums[i+1:]), combinedArr(tmp, []int{nums[i]}))
}
}
func combinedArr(arr1, arr2 []int) []int {
var result []int
result = append(result, arr1...)
result = append(result, arr2...)
return result
}
|
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1, 1, 2]
输出:
[
[1, 1, 2],
[1, 2, 1],
[2, 1, 1]
]
题解
参考题解
#46 中的算法流程如下,因 #47 包含重复元素,需对递归树进行剪枝:
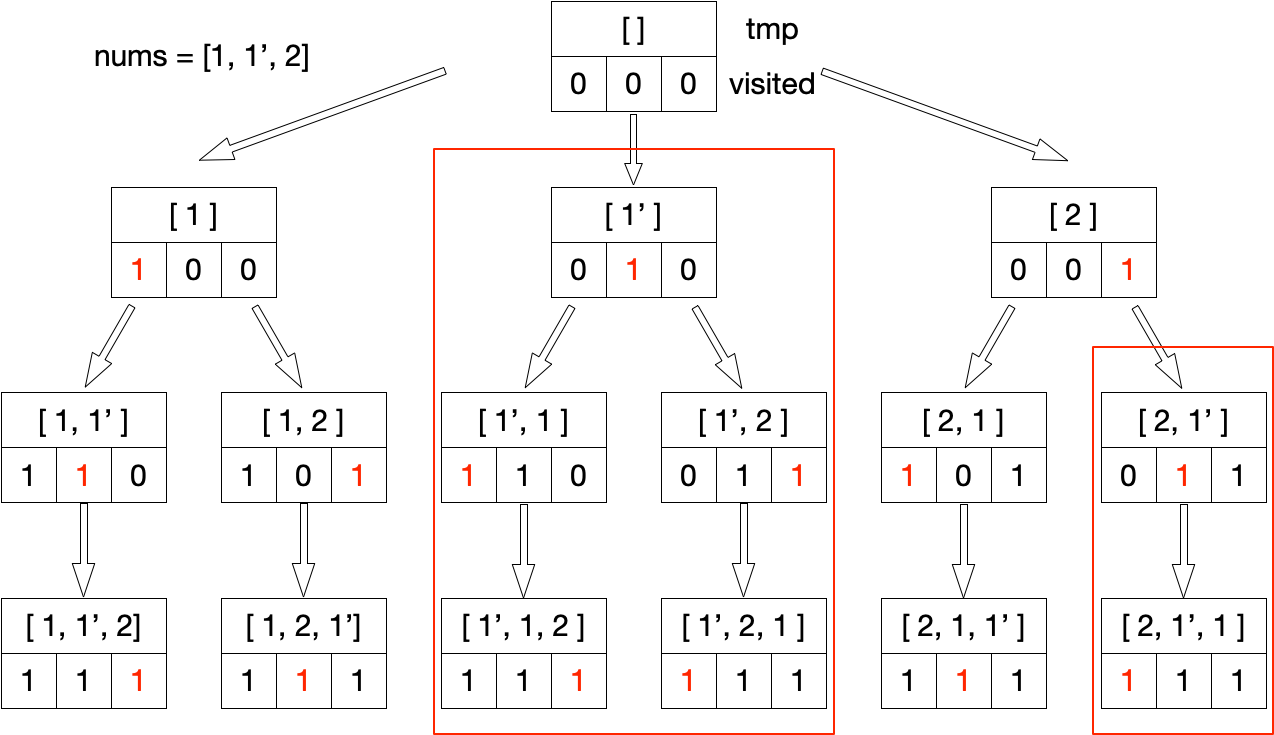
观察可知,若两个分支的前几位排列相同,则这两个分支上的递归子树也相等,如 [1] 与 [1'] 、[2, 1] 与 [2, 1'] (即图上红框中内容)重复,可进行剪枝,在同一层判断 nums[i] == nums[i - 1] 是否成立即可。若只设定这一个剪枝条件,将使以下蓝框中的分支被误剪,导致返回空的解集:
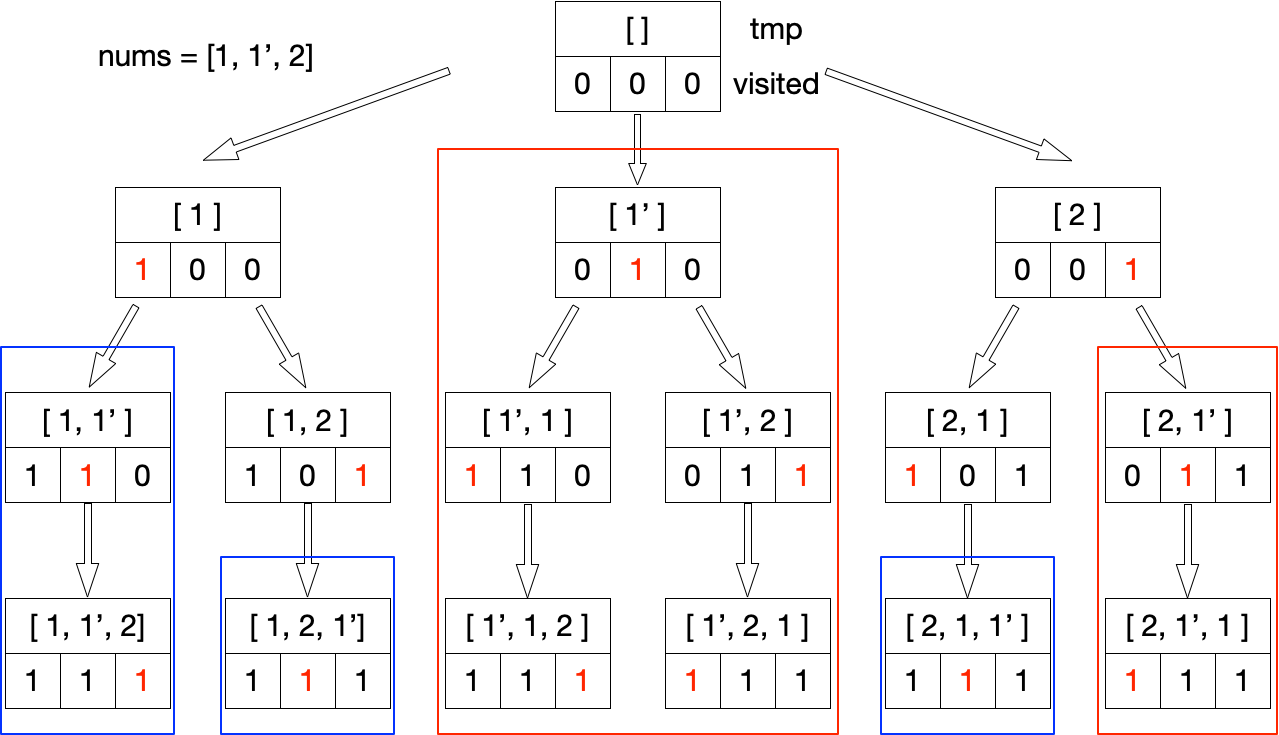
为避免这种现象的产生,可借助 visited 数组对是否遍历过某分支进行标记,仅在前一个分支遍历完成(即 visited[i - 1] == 0 成立时)进行剪枝。故剪枝的判断条件为 i > 0 && nums[i] == nums[i - 1] && visited[i - 1] == 0 。
下图为递归时递归栈的调用顺序:
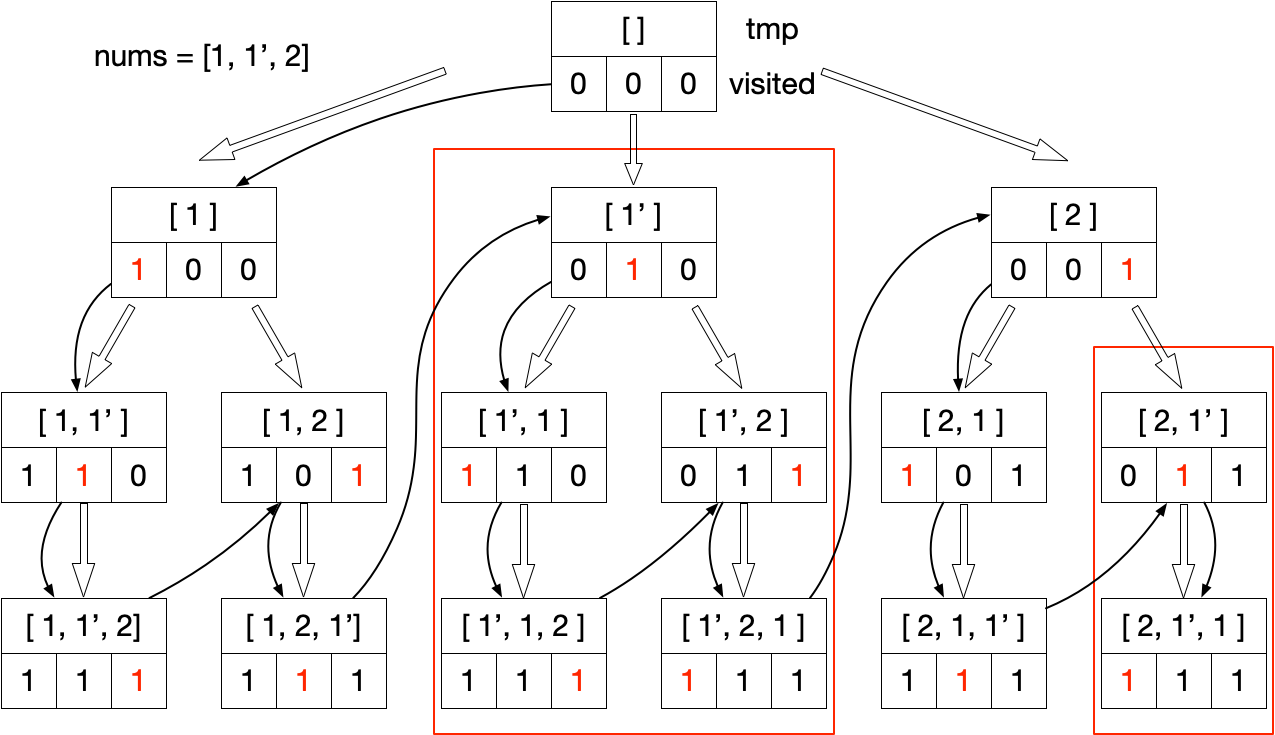
注: 实际上 visited[i - 1] 等于 0、不等于 0、等于 1、不等于 1 四种情况下产生的结果相同,但若直接去掉则将返回空的解集🙃。visited[i - 1] 起到的是标记的作用,即只选择 visited[i - 1] 等于 0 或只选择等于 1 的分支,区别仅在于最终结果集中元素的顺序不同,详见 这篇题解 的补充说明部分。

Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
dfs(res, nums, new ArrayList<>(), new int[nums.length]);
return res;
}
public void dfs(List<List<Integer>> res, int[] nums, List<Integer> tmp, int[] visited) {
if (tmp.size() == nums.length) {
res.add(new ArrayList<>(tmp));
return;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i] == 1) continue;
if (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] == 0) continue;
tmp.add(nums[i]);
visited[i] = 1;
dfs(res, nums, tmp, visited);
visited[i] = 0;
tmp.remove(tmp.size() - 1);
}
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution:
def permuteUnique(self, nums: list) -> list:
results = []
arr_len = len(nums)
def dfs(tmp: list, visited: list):
if len(tmp) == arr_len:
results.append(tmp[:])
return
for i in range(arr_len):
if visited[i] or (i > 0 and nums[i] == nums[i - 1] and not visited[i - 1]): continue
tmp.append(nums[i])
visited[i] = 1
dfs(tmp, visited)
visited[i] = 0
tmp.pop()
nums.sort()
dfs([], [0] * len(nums))
return results
|
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| import "sort"
func permuteUnique(nums []int) [][]int {
var results [][]int
sort.Ints(nums)
arrLen := len(nums)
dfs(&results, nums, []int{}, make([]int, arrLen), arrLen)
return results
}
func dfs(results *[][]int, nums, tmp, visited []int, arrLen int) {
if len(tmp) == arrLen {
*results = append(*results, append([]int{}, tmp...)) // 注意深拷贝
return
}
for i := 0; i < arrLen; i++ {
if visited[i] == 1 || (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] == 0) {
continue
}
tmp = append(tmp, nums[i])
visited[i] = 1
dfs(results, nums, tmp, visited, arrLen)
tmp = tmp[:len(tmp) - 1]
visited[i] = 0
}
}
|
其它解法
仿写 C++ 中的 nextPermutation 函数,该解法 #46、#47 均可 AC。
详见 下一个排列
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| import java.util.*;
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
Arrays.sort(nums);
results.add(arrToList(nums));
while (nextPermutation(nums)) {
results.add(arrToList(nums));
}
return results;
}
public List<Integer> arrToList(int[] nums) {
List<Integer> result = new ArrayList<>();
for (int num : nums) result.add(num);
return result;
}
public boolean nextPermutation(int[] nums) {
int arrLen = nums.length;
int i = arrLen - 2, j = arrLen - 1, k = arrLen - 1;
while (i >= 0 && nums[i] >= nums[j]) {
i--; j--;
}
if (i == -1) return false;
while (nums[i] >= nums[k]) k--;
swap(nums, i, k);
for (i = j, j = arrLen - 1; i < j; i++, j--) {
swap(nums, i, j);
}
return true;
}
public void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution:
def permuteUnique(self, nums: list) -> list:
results = []
arr_len = len(nums)
def next_permutation() -> bool:
i, j, k = arr_len - 2, arr_len - 1, arr_len - 1
while i >= 0 and nums[i] >= nums[j]:
i -= 1
j -= 1
if i == -1: return False
while nums[i] >= nums[k]: k -= 1
nums[i], nums[k] = nums[k], nums[i]
i, j = j, arr_len - 1
while i < j:
nums[i], nums[j] = nums[j], nums[i]
i += 1
j -= 1
return True
nums.sort()
results.append(nums[:])
while next_permutation():
results.append(nums[:])
return results
|
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| import "sort"
func permuteUnique(nums []int) [][]int {
var results [][]int
arrLen := len(nums)
sort.Ints(nums)
results = append(results, append([]int{}, nums...))
for nextPermutation(nums, arrLen) {
results = append(results, append([]int{}, nums...))
}
return results
}
func nextPermutation(nums []int, arrLen int) bool {
i, j, k := arrLen - 2, arrLen - 1, arrLen - 1
for i >= 0 && nums[i] >= nums[j] {
i--
j--
}
if i == -1 {
return false
}
for nums[i] >= nums[k] {
k--
}
nums[i], nums[k] = nums[k], nums[i]
for i, j = j, arrLen - 1; i < j; i, j = i + 1, j - 1 {
nums[i], nums[j] = nums[j], nums[i]
}
return true
}
|



