Leaky Cauldron
0%

组合总和

Posted on Edited on

题目(LeetCode #39)

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

输入： candidates = [2, 3, 6, 7], target = 7,

所求解集为：
[
  [7],
  [2,2,3]
]

示例 2：

输入： candidates = [2,3,5], target = 8,

所求解集为：
[
  [2, 2, 2, 2],
  [2, 3, 3],
  [3, 5]
]

提示：

  • 1 <= candidates.length <= 30
  • 1 <= candidates[i] <= 200
  • candidate 中的每个元素都是独一无二的。
  • 1 <= target <= 500

题解

参考题解

思路分析

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

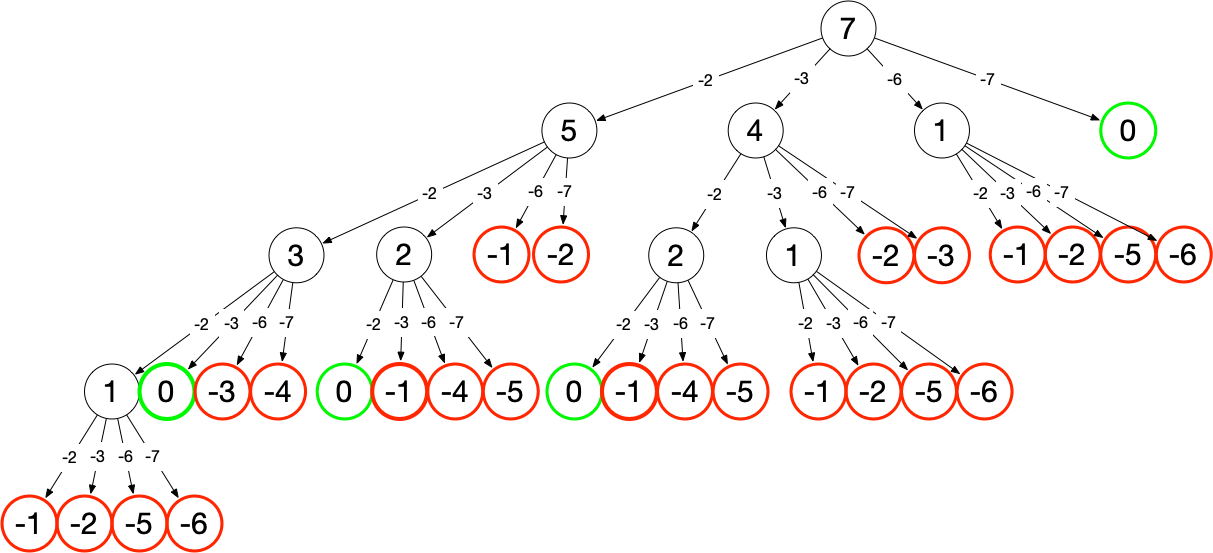
本题为回溯法经典例题，以 candidates = [2, 3, 6, 7] ， target = 7 为例，可用 target 减去 candidates 中的元素，得到新的 target ，再减去 candidates 中的元素，多次相减，若在某次迭代中 target 变为 0，则减数的集合即为一个解；若 target 小于 0 则回退至上一步继续寻找下一个解。如下图所示，其中绿色叶节点所在的路径即为一解。

以上算法实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import java.util.*;

class Solution {
    List<List<Integer>> results = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int arrLen = candidates.length;
        if (arrLen == 0) return results;

        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, arrLen, target, path);
        return results;
    }

    public void dfs(int[] candidates, int begin, int arrLen, int target, Deque<Integer> path) {
        if (target < 0) return;
        if (target == 0) {
            results.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < arrLen; i++) {
            path.addLast(candidates[i]);
            dfs(candidates, i, arrLen, target - candidates[i], path);
            // 回溯，移除路径的最后一段，相当于回到了上一层。
            // 如路径[2, 2, 2, 2]，上一行 dfs 递归遇到 target < 0，返回。
            // 移除路径最后一段 2，即返回了上一层的 1，继续计算 candidates[i] = 3 的情况。
            path.removeLast();
        }
    }
}

输出：

1
2
3
4
[ 2 2 3 ]
[ 2 3 2 ]
[ 3 2 2 ]
[ 7 ]

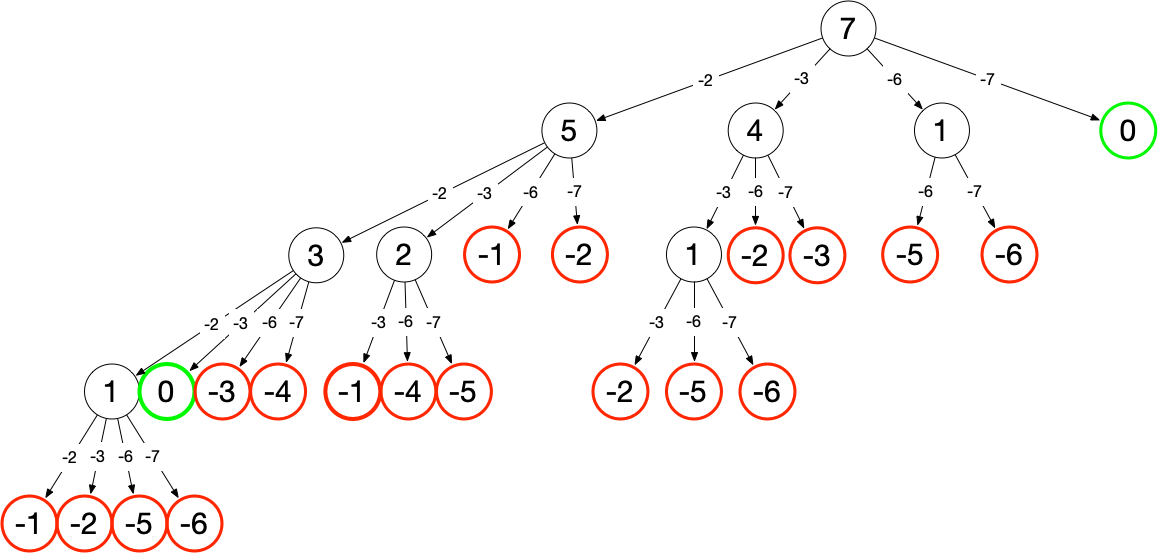
可以看到出现了重复解，这是由于每次计算下一层的 target 时均考虑了 candidates 的所有情况。若要避免这种重复，可在每个分支上排除之前已计算过的 candidates 值，如在 7 - 2 = 5 分支上已考虑了所有 candidates[i] = 2 的情况，在 7 - 3/6/7 三个分支上无需重复考虑。去重后树结构如下：

实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import java.util.*;

class Solution {
    List<List<Integer>> results = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int arrLen = candidates.length;
        if (arrLen == 0) return results;

        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, arrLen, target, path);
        return results;
    }

    public void dfs(int[] candidates, int begin, int arrLen, int target, Deque<Integer> path) {
        if (target < 0) return;
        if (target == 0) {
            results.add(new ArrayList<>(path));
            return;
        }

        // 对 candidates 的循环改为从 begin 位置开始
        // 如遍历到 i = 1 时，后续遍历时也会跳过 i = 0 位置
        for (int i = begin; i < arrLen; i++) {
            path.addLast(candidates[i]);
            dfs(candidates, i, arrLen, target - candidates[i], path);
            path.removeLast();
        }
    }
}

此时输出即为无重复的解：

1
2
[ 2 2 3 ]
[ 7 ]

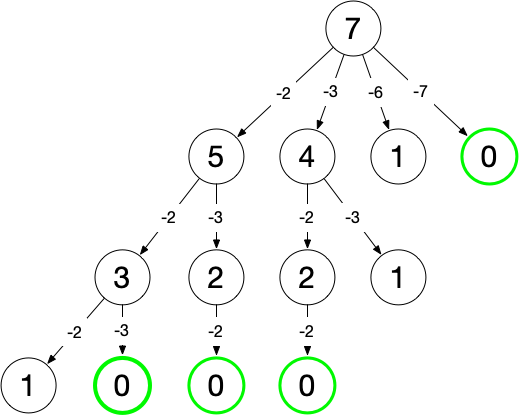
剪枝提速

在计算过程中，若 target 减去某个 candidates[i] 后小于 0，则大于该 candidates[i] 的值与 target 的差也必然小于 0。故可先对 candidates 数组进行升序排序，在遍历 candidates 数组的过程中，若 target < candidates[i] 则 i + 1 及其之后的位置也无需考虑。

注意： 采用这种剪枝方法必须先将 candidates 数组排序，否则若大于 target 的数排在前时，会提前触发 break，导致后边小于 target 的元素被跳过。

剪枝后的树如下，可以看到已减少了很多分支：

实现如下

Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> result = new ArrayList<>();
        if (len == 0) return result;

        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, result);
        return result;
    }

    public void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            if (target < candidates[i]) break;
            path.addLast(candidates[i]);
            dfs(candidates, i, len, target - candidates[i], path, result);
            path.removeLast();
        }
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def __init__(self):
        self.path = []
        self.results = []

    def combinationSum(self, candidates: list, target: int) -> list:
        arr_len = len(candidates)
        if arr_len == 0: return self.results

        candidates.sort()
        self.dfs(candidates, 0, arr_len, target)
        return self.results

    def dfs(self, candidates: list, begin: int, arr_len: int, target: int) -> None:
        if target == 0:
            self.results.append(self.path[:]) # 此处注意需要深拷贝
            return

        for i in range(begin, arr_len):
            if (target - candidates[i] < 0): break
            self.path.append(candidates[i])
            self.dfs(candidates, i, arr_len, target - candidates[i])
            self.path.pop()
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func combinationSum(candidates []int, target int) [][]int {
	arrLen := len(candidates)
	var results [][]int
	if arrLen == 0 {
		return results
	}

	var path []int
	sort.Ints(candidates)
	dfs(candidates, 0, arrLen, target, &results, path)
	return results
}

func dfs(candidates []int, begin, arrLen, target int, results *[][]int, path []int) {
	if target == 0 {
		*results = append(*results, path[:]) // 深拷贝
		return
	}

	for i := begin; i < arrLen; i++ {
		if target - candidates[i] < 0 {
			break
		}

		path = append(path, candidates[i])
		dfs(candidates, i, arrLen, target - candidates[i], results, path)
		path = path[:len(path)-1]
	}
}

进阶(LeetCode #40)

参考题解

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

  • 所有数字（包括目标数）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

输入： candidates = [10, 1, 2, 7, 6, 1, 5], target = 8,

所求解集为：
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2：

输入： candidates = [2, 5, 2, 1, 2], target = 5,

所求解集为：
[
  [1, 2, 2],
  [5]
]

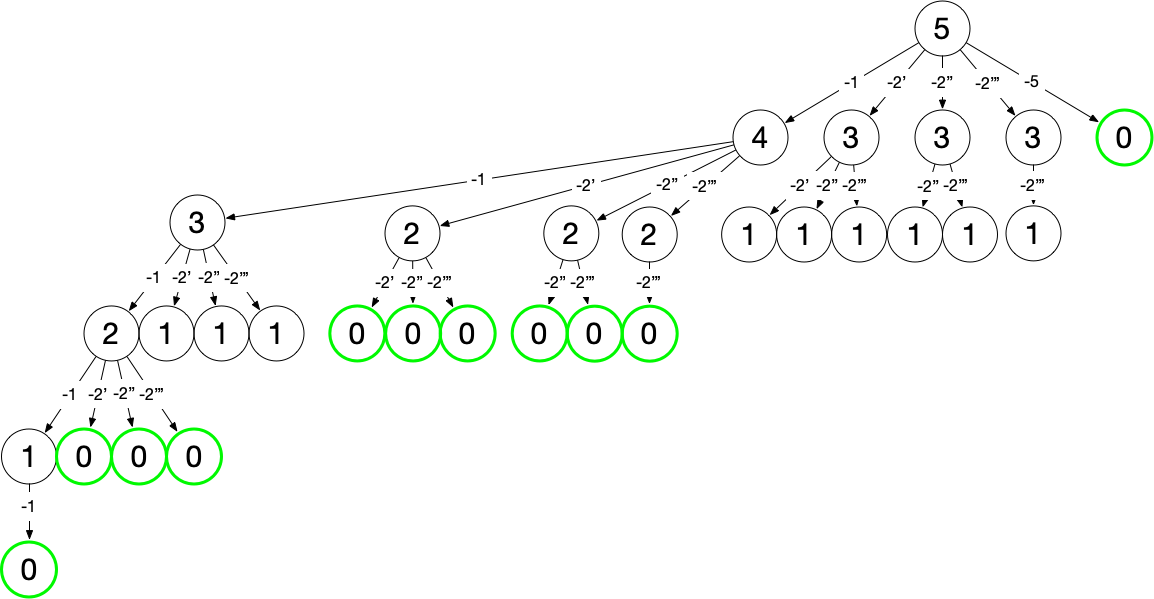
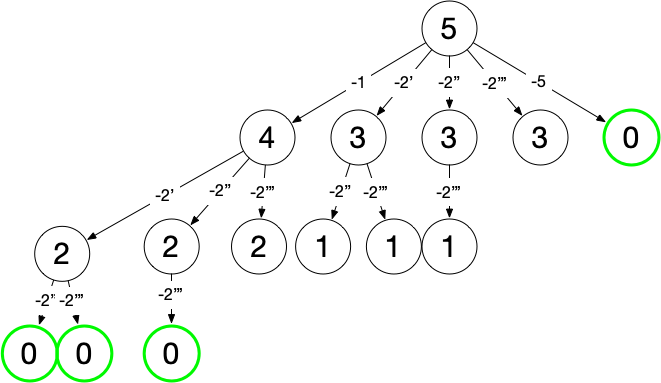
题解

以 candidates = [2, 5, 2, 1, 2] ，target = 5 为例，若采用 #39 题中的算法，得到以下树结构（以 2',2'',2''' 区分三个位置的 2）：

输出如下

1
2
3
4
5
6
7
8
9
10
11
[ 1 1 1 1 1 ]
[ 1 1 1 2 ]
[ 1 1 1 2 ]
[ 1 1 1 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 5 ]

需修改算法使之满足以下两个条件：

  • 每个数字在每个组合中只能使用一次
  • 解集不能包含重复的组合

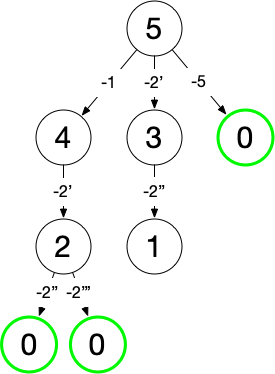
限制组合中数字的出现次数

在分支上遍历 candidates 时跳过已使用过的位置即可，此时树的结构如下：

实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> result = new ArrayList<>();
        if (len == 0) return result;

        // 必须先排序
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, result);
        return result;
    }

    public void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            if (target < candidates[i]) break;
            path.addLast(candidates[i]);
            // 下一层 begin 从 i + 1 开始，跳过当前的 i
            dfs(candidates, i + 1, len, target - candidates[i], path, result);
            path.removeLast();
        }
    }
}

此时输出为：

1
2
3
4
[ 1 2 2 ]
[ 1 2 2 ]
[ 1 2 2 ]
[ 5 ]

去除重复组合

从图中可知组合 [1, 2', 2''] 、[1, 2', 2'''] 和 [1, 2'', 2'''] 三者重复，要去除这种重复应跳过同一层级出现的相等元素。剪枝后的树结构如下：

最终输出为：

1
2
[ 1 2 2 ]
[ 5 ]

实现如下：

Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> result = new ArrayList<>();
        if (len == 0) return result;

        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, result);
        return result;
    }

    public void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = begin; i < len; i++) {
            if (target < candidates[i]) break;
            // 跳过同一层的相等元素
            if (i > begin && candidates[i] == candidates[i - 1]) continue;
            path.addLast(candidates[i]);
            dfs(candidates, i + 1, len, target - candidates[i], path, result);
            path.removeLast();
        }
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def __init__(self):
        self.path = []
        self.results = []

    def combinationSum2(self, candidates: list, target: int) -> list:
        arr_len = len(candidates)
        if arr_len == 0: return self.results

        candidates.sort()
        self.dfs(candidates, 0, arr_len, target)

        return self.results

    def dfs(self, candidates: list, begin: int, arr_len: int, target: int) -> None:
        if target == 0:
            self.results.append(self.path[:]) # 注意此处 path 需要深拷贝
            return

        for i in range(begin, arr_len):
            if target - candidates[i] < 0: break
            if i > begin and candidates[i] == candidates[i - 1]: continue
            self.path.append(candidates[i])
            self.dfs(candidates, i + 1, arr_len, target - candidates[i])
            self.path.pop()
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func combinationSum2(candidates []int, target int) [][]int {
	arrLen := len(candidates)
	var results [][]int
	if arrLen == 0 {
		return results
	}

	var path []int
	sort.Ints(candidates)
	dfs(candidates, 0, arrLen, target, &results, path)
	return results
}

func dfs(candidates []int, begin, arrLen, target int, results *[][]int, path []int) {
	if target == 0 {
		*results = append(*results, append([]int{}, path...))
		return
	}

	for i := begin; i < arrLen; i++ {
		if target < candidates[i] {
			break
		}
		if i > begin && candidates[i] == candidates[i-1] {
			continue
		}

		path = append(path, candidates[i])
		dfs(candidates, i+1, arrLen, target-candidates[i], results, path)
		path = path[:len(path)-1]
	}
}