给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例1:
输入: nums = [5,7,7,8,8,10], target = 8输出: [3,4]
示例2:
输入: nums = [5,7,7,8,8,10], target = 6输出: [-1, -1]
题解 方法一 先进行二分查找找到目标值 target ,再从两侧逐位逼近 mid ,判断是否与 target 相等即可找到开始合结束位置。
查找阶段时间复杂度为 O(logn) ,但在查找首尾时若输入数组全部为 target ,如 [8, 8, 8, 8 , 8] ,则将退化至 O(n) 。
Java 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { public int [] searchRange(int [] nums, int target) { if (nums == null || nums.length == 0 ) return new int []{-1 , -1 }; int arrLen = nums.length; int left = 0 , right = arrLen - 1 ; while (left <= right) { int mid = (left + right) / 2 ; if (nums[mid] == target) { while (nums[left] != target) left++; while (nums[right] != target) right--; return new int []{left, right}; } if (nums[mid] < target) left = mid + 1 ; else right = mid - 1 ; } return new int []{-1 , -1 }; } }
Python 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution : def searchRange (self, nums: list , target: int ) -> list : if not nums or len (nums) == 0 : return [-1 , -1 ] arr_len = len (nums) left , right = 0 , arr_len - 1 while left <= right: mid = (left + right) // 2 if nums[mid] == target: while nums[left] != target: left += 1 while nums[right] != target: right -= 1 return [left, right] if nums[mid] < target: left = mid + 1 else : right = mid - 1 return [-1 , -1 ]
Go 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 func searchRange (nums []int , target int ) int { arrLen := len (nums) if arrLen == 0 { return []int {-1 , -1 } } left, right := 0 , arrLen - 1 for left <= right { mid := (left + right) / 2 if nums[mid] == target { for nums[left] != target { left++ } for nums[right] != target { right-- } return []int {left, right} } if nums[mid] < target { left = mid + 1 } else { right = mid - 1 } } return []int {-1 , -1 } }
方法二 在方法一的基础上,在查找首尾时也采用二分查找,时间复杂度整体为 O(logn) 。
与一般的二分法查找相等位置不同,查找起始位置的终止条件为:前一个元素与当前元素不相等;查找终止位置的结束条件为:后一个元素与当前元素不相等。
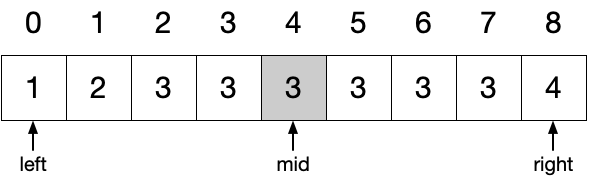
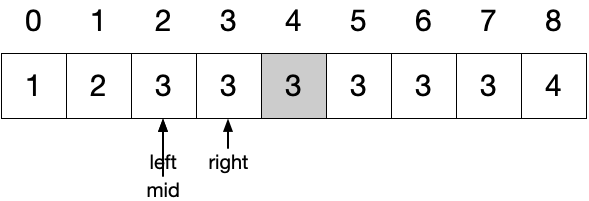
以输入 nums = [1, 2, 3, 3, 3, 3, 3, 3, 4] 和 target = 3 ,查找目标值的开始位置为例。
首先根据二分法找到与 target 相等的位置,在此即为 4 。
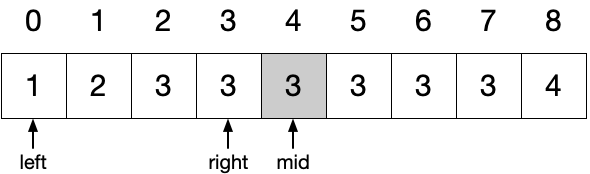
由于有 nums[mid] == nums[mid - 1] ,将 right 指向 mid - 1 。
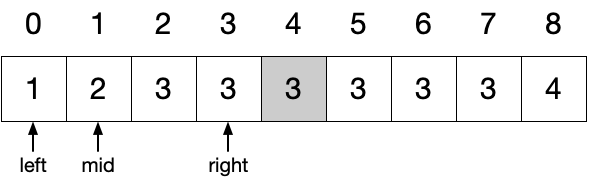
重新计算 mid 为 3 // 2 = 1 。
此时有 nums[mid] < target ,将 left 指向 mid + 1 。
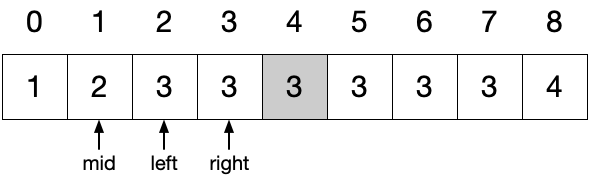
重新计算 mid 为 2,此时 nums[mid] != nums[mid - 1] ,返回 mid 当前值即为目标值的开始位置。
查找 target 的结束位置与上述过程类似,不再赘述。
Java 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { public int [] searchRange(int [] nums, int target) { return new int [] { binarySearch(nums, target, true ), binarySearch(nums, target, false ) }; } public int binarySearch (int [] nums, int target, boolean isSearchFirst) { int arrLen = nums.length; if (arrLen == 0 ) return -1 ; int left = 0 , right = arrLen - 1 ; while (left <= right) { int mid = (left + right) / 2 ; if (nums[mid] < target) left = mid + 1 ; else if (nums[mid] > target) right = mid - 1 ; else { if (isSearchFirst) { if (mid > 0 && nums[mid] == nums[mid - 1 ]) right = mid - 1 ; else return mid; } else { if (mid < arrLen - 1 && nums[mid] == nums[mid + 1 ]) left = mid + 1 ; else return mid; } } } return -1 ; } }
Python 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution : def searchRange (self, nums: list , target: int ) -> list : if not nums or len (nums) == 0 : return [-1 , -1 ] return [ self.binary_search(nums, target, True ), self.binary_search(nums, target, False ) ] def binary_search (self, nums: list , target: int , is_search_first: bool ): arr_len = len (nums) left, right = 0 , arr_len - 1 while left <= right: mid = (left + right) // 2 if nums[mid] > target: right = mid - 1 elif nums[mid] < target: left = mid + 1 else : if is_search_first: if mid > 0 and nums[mid] == nums[mid - 1 ]: right = mid - 1 else : return mid else : if mid < arr_len - 1 and nums[mid] == nums[mid + 1 ]: left = mid + 1 else : return mid return -1
Go 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 func searchRange (nums []int , target int ) int { return []int { binarySearch(nums, target, true ), binarySearch(nums, target, false ), } } func binarySearch (nums []int , target int , isSearchFirst bool ) int { arrLen := len (nums) if arrLen == 0 { return -1 } left, right := 0 , arrLen - 1 for left <= right { mid := (left + right) / 2 if nums[mid] < target { left = mid + 1 } else if nums[mid] > target { right = mid - 1 } else { if isSearchFirst { if mid > 0 && nums[mid] == nums[mid - 1 ] { right = mid -1 } else { return mid } } else { if mid < arrLen - 1 && nums[mid] == nums[mid + 1 ] { left = mid + 1 } else { return mid } } } } return -1 }