下一个排列

题目(LeetCode #31)

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。

1
2
3

1,2,3 -> 1,3,2
3,2,1 -> 1,2,3
1,1,5 -> 1,5,1

题解

参考题解

仿照 C++ 中 next_permutation 的实现方法。

分析

下一个数比当前数大：将后面的大数与前面的小数交换 ，如 123456 ，将 5 和 6 交换得到 123465 ；
下一个数的增幅应尽量小，使之满足字典序中的 下一个，为了满足该条件需进行如下操作：
1. 在 尽可能靠右的低位进行交换，需从后向前查找；
2. 将一个尽可能小的大数与前面的小数交换，如 123465 ，下一个排列应该将 5 与 4 交换而不是将 6 和 4 交换；
3. 将大数换到前面后，需将大数后面的所有数重置为升序，升序排列即为最小排列。以 123465 为例：首先按照上一步，交换 5 和 4 ，得到 123564 。调整 5 后的数为升序，得到 123546 ，即为下一个排列。

实现步骤

从后向前查找第一个相邻升序的元素对 (i, j) ，满足 nums[i] < nums[j] 。此时 [j, end) 必然为降序；
在 [j, end) 从后向前查找第一个满足 nums[i] < nums[k] 的 k 。nums[i] 和 nums[k] 即为上述小数和大数；
交换 nums[i] 和 nums[k] ；
此时 [j, end) 必然为降序，逆置 [j, end) 使其升序；
若在步骤 1 找不到符合的相邻元素对，则说明当前数组单调递减，直接跳到步骤 4，整体逆序即可。

图解

以求 12385764 的下一个排列为例：

初始时：
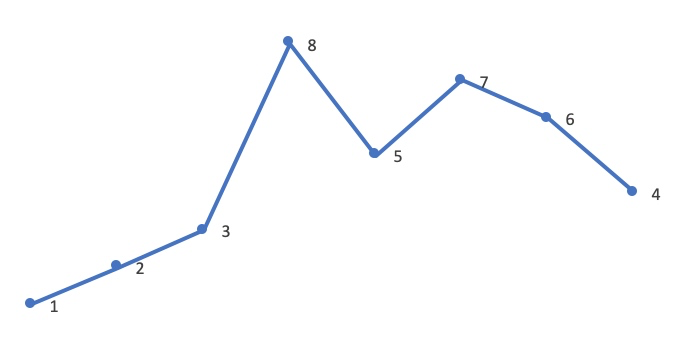
从后向前查找第一个相邻升序的元素对 (i, j) ，这里 i=4 ，j=5 ，对应值为 5 和 7 ：
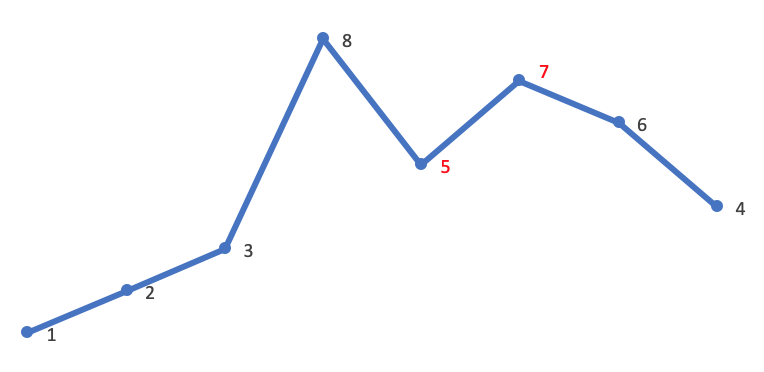
从后向前查找第一个大于 nums[i] 的值 nums[k] ，此例中 nums[i] = 5 ，故 nums[k]=6
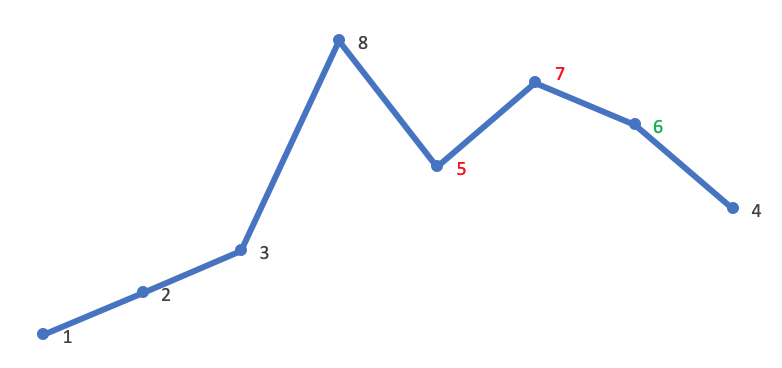
交换 nums[i] 和 nums[k] ，即 5 和 6：
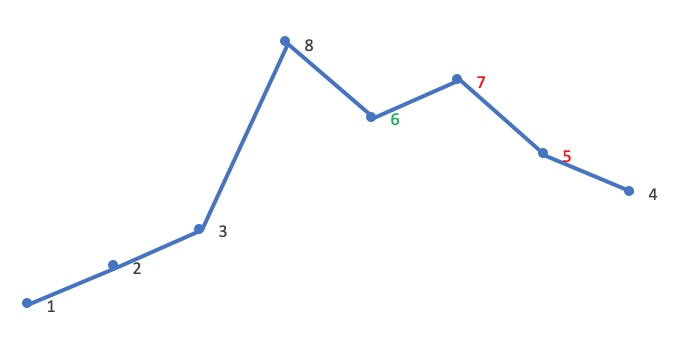
交换后 [j, end) 必仍是降序，逆置 [j, end) ，使其变为升序：
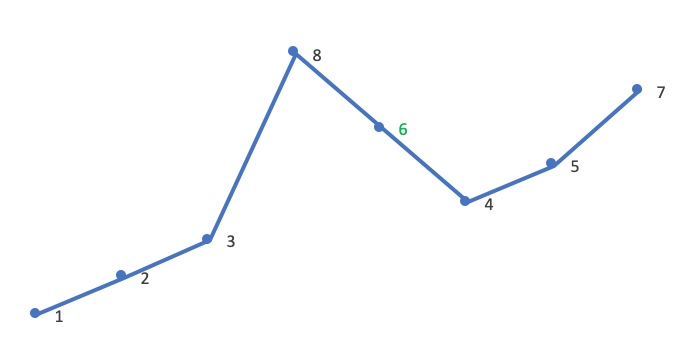
故 12385764 的下一个排列为 12386457 ，逆序后对比如下：

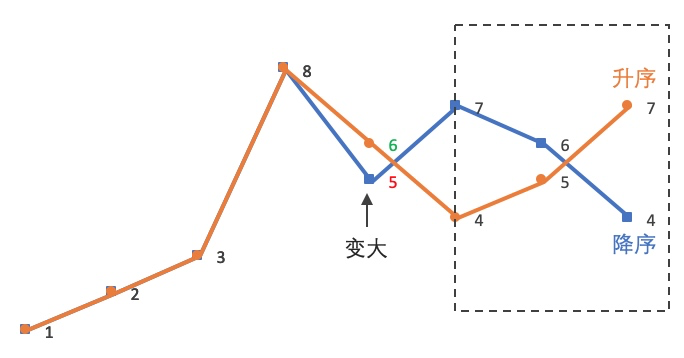
实现

Java

class Solution {
    public void nextPermutation(int[] nums) {
        int arrLen = nums.length;
        if (arrLen <= 1) return;

        int i = arrLen - 2, j = arrLen - 1, k = arrLen - 1;

        while (i >= 0 && nums[i] >= nums[j]) {
            i--; j--;
        }

        if (i >= 0) {
            while (nums[i] >= nums[k]) k--;
            swap(i, k, nums);
        }

        for (i = j, j = arrLen - 1; i < j; i++, j--) {
            swap(i, j, nums);
        }
    }

    public void swap(int i, int j, int[] nums) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

Python

class Solution:
    def nextPermutation(self, nums: list) -> None:
        arr_len = len(nums)
        if arr_len <= 1: return

        i, j, k = arr_len - 2, arr_len - 1, arr_len - 1

        while i >= 0 and nums[i] >= nums[j]:
            i -= 1
            j -= 1

        if i >= 0:
            while nums[i] >= nums[k]: k -= 1
            nums[i], nums[k] = nums[k], nums[i]

        i, j = j, arr_len - 1
        while i < j:
            nums[i], nums[j] = nums[j], nums[i]
            i += 1
            j -= 1

Go

func nextPermutation(nums []int)  {
    arrLen := len(nums)
    if arrLen <= 1 {
        return
    }

    i, j, k := arrLen - 2, arrLen - 1, arrLen - 1
    for i >= 0 && nums[i] >= nums[j] {
        i--
        j--
    }

    if i >= 0 {
        for nums[i] >= nums[k] {
            k--
        }
        nums[i], nums[k] = nums[k], nums[i]
    }

    i, j = j, arrLen - 1
    for i < j {
        nums[i], nums[j] = nums[j], nums[i]
        i++
        j--
    }
}