Leaky Cauldron
0%

二叉查找树

Posted on Edited on

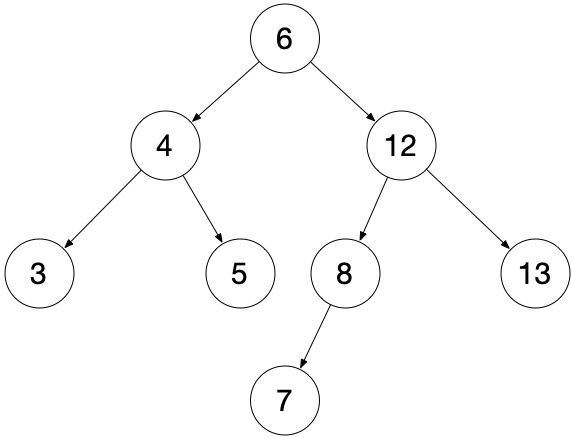
定义

二叉查找树，也称为二叉搜索树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

  1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；
  3. 任意节点的左、右子树也分别为二叉查找树；

其优势在于查找、插入的时间复杂度较低，理想情况下为 O(logn) 。

实现

节点定义

1
2
3
4
5
6
7
8
9
10
11
12
13
class Node {
    int value;
    Node parent;
    Node left;
    Node right;

    public Node(int value, Node parent, Node left, Node right) {
        this.value = value;
        this.parent = parent;
        this.left = left;
        this.right = right;
    }
}

查找节点

1
2
3
4
5
6
7
8
9
10
11
12
13
public static Node search(int ele) {
    Node tmp = root;

    while (tmp != null && tmp.value != ele) {
        if (ele < tmp.value) {
            tmp = tmp.left;
        } else {
            tmp = tmp.right;
        }
    }

    return tmp;
}

插入节点

先找到待插入节点的父节点，再插入新节点并返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static Node insert(int ele) {
    if (root == null) {
        root = new Node(ele, null, null, null);
        return root;
    }

    // 找到即将插入元素的父节点
    Node parent = null;
    Node tmp = root;
    while (tmp != null) {
        parent = tmp;
        if (ele < tmp.value) {
            tmp = tmp.left;
        } else {
            tmp = tmp.right;
        }
    }

    Node newNode = new Node(ele, parent, null, null);
    if (parent.value > ele) {
        parent.left = newNode;
    } else {
        parent.right = newNode;
    }

    return newNode;
}

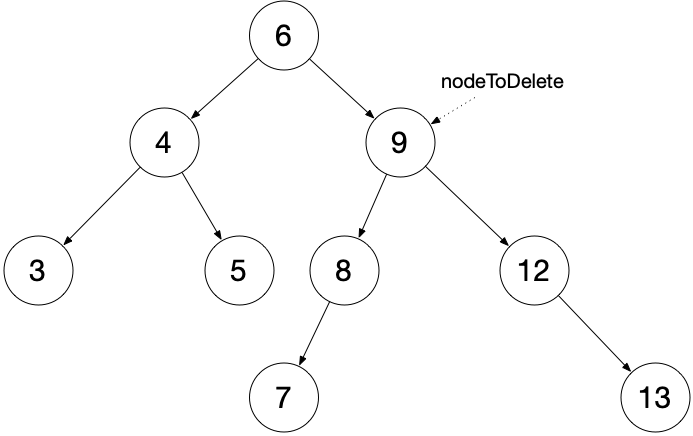
删除节点

替换 / 移植节点

使用 newNode 替换 nodeToReplace ，并返回被替换的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static Node transplant(Node nodeToReplace, Node newNode) {
    if (nodeToReplace.parent == null) {
        root = newNode;
    } else if (nodeToReplace == nodeToReplace.parent.left) {
        nodeToReplace.parent.left = newNode;
    } else {
        nodeToReplace.parent.right = newNode;
    }

    if (newNode != null) {
        newNode.parent = nodeToReplace.parent;
    }

    return newNode;
}

找到后继节点

找到节点的中序后继，即该节点右子树上的最小值。

1
2
3
4
5
6
7
public static Node getMinimum(Node node) {
    while (node.left != null) {
        node = node.left;
    }

    return node;
}

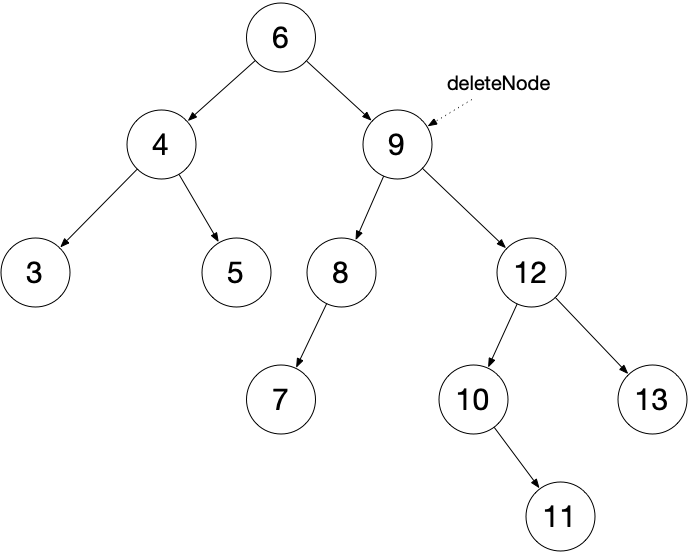
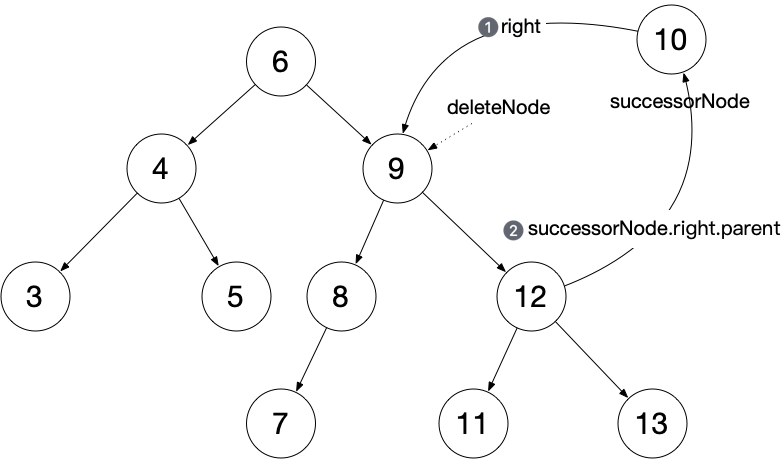
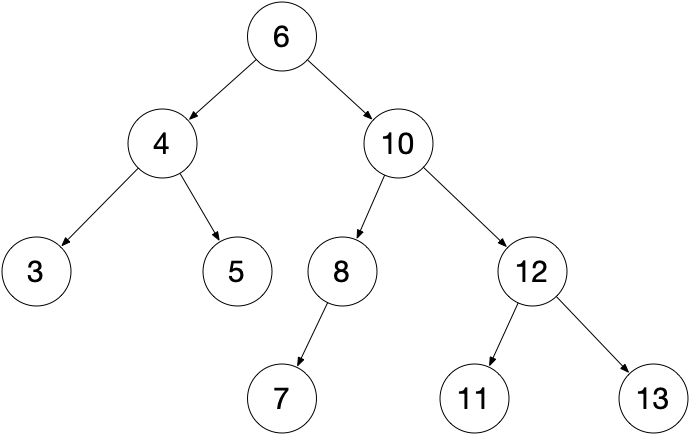
删除

将待删除节点的中序后继移动到待删除节点位置，并调整树的结构

  • 若待删除节点的父节点无左子树或右子树，直接将该节点的右子树或左子树上移即可；

  • 若待删除节点的左右子树均不为空，以下图所示树为例，其中 9 为待删除节点，此时其中序后继 10 与 9 不直接相连

    • 先找到待删除节点的中序后继，在此为 10，即为待删除节点的替换节点，此时该后继不与待删除节点直接相连，先将其子树 11 移至 10 位置。①使 successorNode.right 指向待删除节点 9 的 right ，②使 successorNode.right.parent 指向 10，得到：

    • 再将 successorNode 移到 deleteNode 的位置，并修改其左子树的指向。

  • 若中序后继与待删除节点直接相连，如下图所示：

    • 9 与 12 直接相连，则直接将 12 上移至 9 的位置，并修改 12 的左子树指向即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static Node delete(Node deleteNode) {
    if (deleteNode != null) {
        Node nodeToReturn = null;
        if (deleteNode.left == null) {
            nodeToReturn = transplant(deleteNode, deleteNode.right);
        } else if (deleteNode.right == null) {
            nodeToReturn = transplant(deleteNode, deleteNode.left);
        } else {
            Node successorNode = getMinimum(deleteNode.right);
            if (successorNode.parent != deleteNode) {
                transplant(successorNode, successorNode.right);
                successorNode.right = deleteNode.right;
                successorNode.right.parent = successorNode;
            }
            transplant(deleteNode, successorNode);
            successorNode.left = deleteNode.left;
            successorNode.left.parent = successorNode;
            nodeToReturn = successorNode;
        }
        return nodeToReturn;
    }
    return null;
}

缺点

插入或删除节点过程中如果不及时调整，将使查找效率降低，如将数组 [2, 3, 4, 5, 6] 插入树的过程中，不加调整将得到如下结构，此时查找和插入效率退化至 O(n) 。

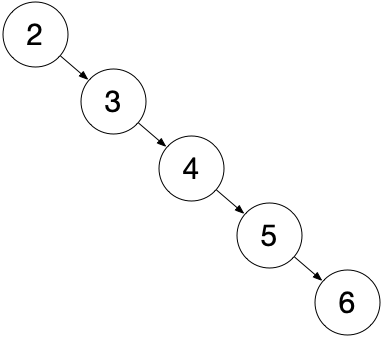
为解决查找效率退化的问题，又提出了 AVL 树和红黑树等，可将最坏效率降至 O(logn)。

完整代码