Leaky Cauldron
0%

Morris遍历

Posted on Edited on

原理

无论是手动创建栈遍历树还是递归（即调用系统栈）遍历树，其空间复杂度均为 O(N) ，而 Morris 实现了 O(1) 常数空间复杂度的树的遍历。

递归遍历树的过程中，每个节点均被遍历了三次，前中后序取决于打印的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class RecursiveTraversal {
    public static void recursiveTraverse(TreeNode head) {
        if (head == null) return;

        // 先序遍历
        // System.out.println(head.val);

        recursiveTraverse(head.left);

        // 中序遍历
        // System.out.println(head.val);
        
        recursiveTraverse(head.right);
        
        // 后序遍历
        // System.out.println(head.val);
    }
}

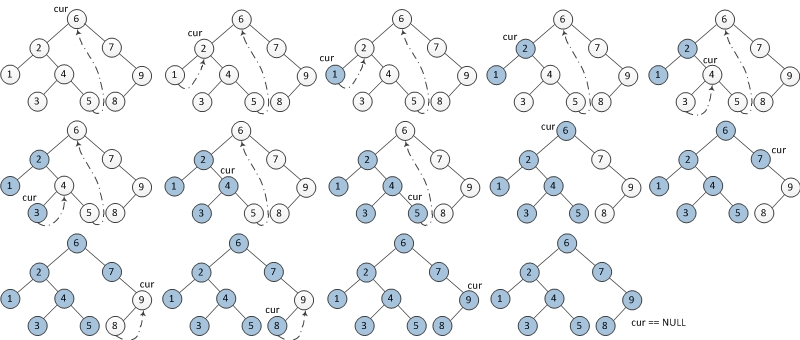
Morris 遍历实质上是人为地追踪递归过程中遍历位置的变化。其过程如下：

设 cur 为当前节点。

  1. 若 cur 无左子树，cur 向右移动
  2. 若 cur 有左子树，找到左子树上最右节点，记为 rightmost
    1. 若 rightmost 的右孩子为 null ，rightmost.right = cur ，cur 向左移动
    2. 若 rightmost 的右孩子为 cur ，rightmost.right = null ，cur 向右移动

  • 若某节点有左子树，则该节点将被遍历两次（即 2.2 ），若没有左子树则将被遍历一次；

  • 在第二遍历某节点时，当前节点总是该节点左子树的 rightmost 的后继（节点的后继指中序遍历输出结果的后续节点）

  • 通过 rightmost 的右孩子的指向来判断是第一次还是第二次遍历到当前节点。

下图为每一步迭代的结果（从左至右，从上到下），cur代表当前节点，深色节点表示该节点已输出。（图源：AnnieKim）

实现

先序遍历

第一次到达一个节点时就输出。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class MorrisTraversal {
    public static void morrisPreorderTraverse(TreeNode head) {
        if (head == null) return;

        TreeNode cur1 = head;
        TreeNode cur2 = null;

        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {                       // cur1 有左子树
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;                // 左子树上最右节点, 此时 cur2 即为 rightmost
                }
                if (cur2.right == null) {             // rightmost 的右孩子为空, 此时为第一次遍历当前节点
                    cur2.right = cur1;
                    System.out.print(cur1.val + " "); // 第一次遍历一个节点, 打印该节点
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;                // rightmost 的右孩子指向 cur1, 此时为第二次遍历当前节点
                }
            } else {
                System.out.print(cur1.val + " ");     // 节点无左子树, 只会遍历一遍, 故直接输出
            }
            cur1 = cur1.right;                        // cur1 无左子树或 rightmost 的右孩子指向 cur1 时
        }
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


def morris_preorder_traverse(head: TreeNode) -> None:
    if not head: return

    cur1 = head
    while cur1:
        cur2 = cur1.left
        if cur2:
            while cur2.right and cur2.right != cur1:
                cur2 = cur2.right
            if cur2.right is None:
                cur2.right = cur1
                print(cur1.val, end=" ")
                cur1 = cur1.left
                continue
            else:
                cur2.right = None
        else:
            print(cur1.val, end=" ")
        cur1 = cur1.right

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
type TreeNode struct {
	val   int
	left  *TreeNode
	right *TreeNode
}

func morrisPreorderTraverse(head *TreeNode) {
	if head == nil {
		return
	}

	cur1 := head
	var cur2 *TreeNode

	for cur1 != nil {
		cur2 = cur1.left
		if cur2 != nil {
			for cur2.right != nil && cur2.right != cur1 {
				cur2 = cur2.right
			}
			if cur2.right == nil {
				cur2.right = cur1
				fmt.Printf("%d ", cur1.val)
				cur1 = cur1.left
				continue
			} else {
				cur2.right = nil
			}
		} else {
			fmt.Printf("%d ", cur1.val)
		}
		cur1 = cur1.right
	}
}

中序遍历

有左子树的节点第二次回到该节点时再打印；无左子树的节点只会遍历一次，故直接输出。如下图输出顺序为 2 1 3 。

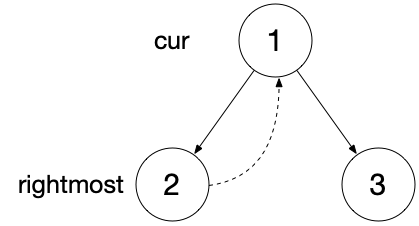
当前节点无左子树或第二次遍历当前节点（即 rightmost 的右孩子指向 cur1）时均需输出当前节点值，而只有这两种情况需将指针右移，故可理解为只要向右移动就输出。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class MorrisTraversal {
    public static void morrisInOrderTraverse(TreeNode head) {
        if (head == null) return;

        TreeNode cur1 = head;
        TreeNode cur2 = null;

        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {               // cur1 有左子树
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;        // 左子树上最右节点, 此时 cur2 即为 rightmost
                }
                if (cur2.right == null) {     // rightmost 的右孩子为空, 此时为第一次遍历当前节点
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;        // rightmost 的右孩子指向 cur1, 此时为第二次遍历当前节点
                }
            }
            System.out.print(cur1.val + " "); // 当前节点无左子树或第二次遍历当前节点
            cur1 = cur1.right;                // cur1 无左子树或 rightmost 的右孩子指向 cur1 时
        }
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def morris_in_order_traverse(head: TreeNode) -> None:
    if not head: return

    cur1 = head
    while cur1:
        cur2 = cur1.left
        if cur2:
            while cur2.right and cur2.right != cur1:
                cur2 = cur2.right
            if cur2.right is None:
                cur2.right = cur1
                cur1 = cur1.left
                continue
            else:
                cur2.right = None
        print(cur1.val, end=" ")
        cur1 = cur1.right

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func morrisInOrderTraverse(head *TreeNode) {
	if head == nil {
		return
	}

	cur1 := head
	var cur2 *TreeNode

	for cur1 != nil {
		cur2 = cur1.left
		if cur2 != nil {
			for cur2.right != nil && cur2.right != cur1 {
				cur2 = cur2.right
			}
			if cur2.right == nil {
				cur2.right = cur1
				cur1 = cur1.left
				continue
			} else {
				cur2.right = nil
			}
		}
		fmt.Printf("%d ", cur1.val)
		cur1 = cur1.right
	}
}

后序遍历

第二次遍历到某节点时，逆序打印其左子树的右边界。遍历完后再逆序打印整棵树的右边界即为后序遍历。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class MorrisTraversal {
    public static void morrisPostOrderTraverse(TreeNode head) {
        if (head == null) return;

        TreeNode cur1 = head;
        TreeNode cur2 = null;

        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {             // cur1 有左子树
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;      // 左子树上最右节点, 此时 cur2 即为 rightmost
                }
                if (cur2.right == null) {   // rightmost 的右孩子为空, 此时为第一次遍历当前节点
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {
                    cur2.right = null;      // rightmost 的右孩子指向 cur1, 此时为第二次遍历当前节点
                    printEdge(cur1.left);   // 第二次遍历到该节点, 打印左子树的右边界
                }
            }
            cur1 = cur1.right;              // cur1 无左子树
        }
        printEdge(head);                    // 打印整棵树的右边界
    }

    public static void printEdge(TreeNode head) {
        TreeNode tail = reverseEdge(head);
        TreeNode cur = tail;

        while (cur != null) {
            System.out.print(cur.val + " ");
            cur = cur.right;
        }
        recursiveTraverse(tail);
    }

    public static TreeNode reverseEdge(TreeNode from) {
        TreeNode pre = null;
        TreeNode next = null;

        while (from != null) {
            next = from.right;
            from.right = pre;
            pre = from;
            from = next;
        }
        return pre;
    }
}

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def morris_post_order_traverse(head: TreeNode) -> None:
    if not head: return

    cur1 = head
    while cur1:
        cur2 = cur1.left
        if cur2:
            while cur2.right and cur2.right != cur1:
                cur2 = cur2.right
            if cur2.right is None:
                cur2.right = cur1
                cur1 = cur1.left
                continue
            else:
                cur2.right = None
                print_edge(cur1.left)
        cur1 = cur1.right
    print_edge(head)


def print_edge(head: TreeNode) -> None:
    tail = reverse_edge(head)
    cur = tail

    while cur:
        print(cur.val, end=" ")
        cur = cur.right

    reverse_edge(tail)


def reverse_edge(head: TreeNode) -> TreeNode:
    pre = None
    while head:
        rear = head.right
        head.right = pre
        pre = head
        head = rear
    return pre

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
func morrisPostOrderTraverse(head *TreeNode) {
	if head == nil {
		return
	}

	cur1 := head
	var cur2 *TreeNode

	for cur1 != nil {
		cur2 = cur1.left
		if cur2 != nil {
			for cur2.right != nil && cur2.right != cur1 {
				cur2 = cur2.right
			}
			if cur2.right == nil {
				cur2.right = cur1
				cur1 = cur1.left
				continue
			} else {
				cur2.right = nil
				printEdge(cur1.left)
			}
		}
		cur1 = cur1.right
	}
	printEdge(head)
}

func printEdge(head *TreeNode) {
	tail := reverseEdge(head)
	cur := tail

	for cur != nil {
		fmt.Printf("%d ", cur.val)
		cur = cur.right
	}

	reverseEdge(tail)
}

func reverseEdge(head *TreeNode) *TreeNode {
	var pre *TreeNode
	for head != nil {
		next := head.right
		head.right = pre
		pre = head
		head = next
	}

	return pre
}