Leaky Cauldron
0%

Manacher算法

Posted on Edited on

题目(LeetCode #5)

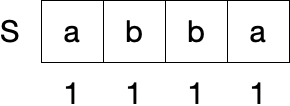
给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：

输入: “cbbd”
输出: “bb”

题解

扩展中心法

遍历字符串，由每个字符串向两侧扩展逐一比对。

时间复杂度为 O(n²) 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() <= 1) return s;

        int begin = 0, maxLen = 1;
        for (int i = 0; i < s.length(); i++) {
            int oddLen = expandAroundCenter(s, i, i);
            int evenLen = expandAroundCenter(s, i, i + 1);
            int curLen = Math.max(oddLen, evenLen);

            if (curLen > maxLen) {
                maxLen = curLen;
                begin = i - (maxLen - 1) / 2; // (maxLen - 1) / 2 向下取整
            }
        }

        return s.substring(begin, begin + maxLen);
    }

    private int expandAroundCenter(String s, int l, int r) {
        while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
            l--; r++;
        }

        return r - l - 1; // 此时 l 指向回文子串前一位，r 指向回文子串后一位
    }
}

Manacher算法

预处理

在原始字符串的每个字符的左右两边都加上特殊字符，使处理后的字符串长度均为奇数，以此来解决偶回文时用扩展法不能找到回文中心而导致的找不到回文子串的问题。

处理前

处理后

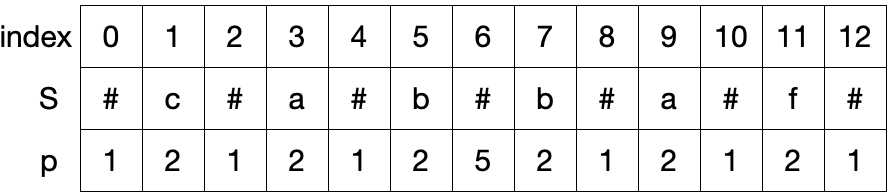
最长回文子串长度

下表中 p 数组存储的是以各字符为中心的回文子串的最大长度。观察可知，预处理后的字符串的最长回文子串的回文半径减 1 即为原字符串的最长回文子串长度。以字符串 cabbaf 为例，处理后的最长回文子串的回文半径为 p[6] = 5 ，p[6] - 1 = 4 即为原字符串的最长回文子串 abba 的长度。

所以原字符串的最长回文子串长度 maxLen = p[i] - 1

最长回文子串的起始索引

在 #c#a#b#b#a#f# 中，p[6] = 5 ，用索引 i 减去最长回文半径 p[i] 即可得到原字符串的最长回文子串的起始索引，即 i - p[i] = 6 - 5 = 1 ；但对奇回文 aba 来说，用这种方法得到的结果为 3 - p[3] = 3 - 4 = -1 ，下标越界。

为解决下标越界的问题，可在预处理后的字符串前再添加一个特殊字符，而为了使字符串长度保持为奇数，其后也需添加另一个字符。而原字符串的最长回文子串的起始索引变为 (i - p[i]) / 2 。

对 cabbaf 来说，原字符串的最长回文子串的起始索引为 (7 - p[7]) / 2 = (7 - 5) / 2 = 1

对 aba 来说，原字符串的最长回文子串的起始索引为 (3 - p[3]) / 2 = (3 - 3) / 2 = 0

故原字符串的最长回文子串的起始索引可表示为 index = (i - p[i]) / 2

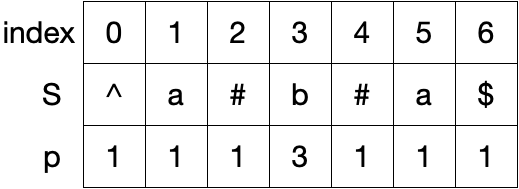
计算 p 数组

定义两个变量 C 和 R ，分别为某一回文子串的中心字符的索引和右边界。如对 ^#c#a#b#b#a#f#$ 中的 #a#b#b#a# 来说，C = 7 ，p[C] = 5 ，以 7 为中心的回文子串的右边界即为 R = C + p[C] = 12 ；当 C = 12 时，以 12 为中心的回文子串的右边界即为 R = C + p[C] = 12 + 2 = 14 。

故可得回文子串右边界与其半径之间的关系为：R = C + p[C]

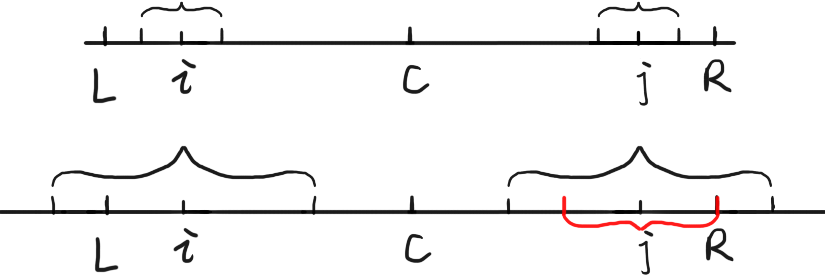
由于回文子串关于 C 对称，由该子串上某位置 i 可得其对称位置 j ，由 i + j = 2 * C 知 j = 2 * C - i 。

  • 若以 j 为中心的回文子串的右边界在 R 以内，即 j + p[j] < R 时，由对称性可知，p[j] = p[i] ；
  • 若以 j 为中心的回文子串的右边界大于 R ，即 j + p[j] > R 时，图中红色部分为关于 j 对称的回文子串，故此时有 p[j] = R - j ；
  • 若 j + p[j] >= R ，则令 p[j] = 1 ，此时也需更新 C 和 R ，继续向后用扩展中心法计算 p 各位置的值。
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class Manacher {
    public String preprocess(String s) {
        String result = "^";
        for (int i = 0; i < s.length(); i++) {
            result += "#" + s.charAt(i);
        }

        return result + "#$";
    }

    public String longestPalindrome(String s) {
        if (s.length() == 0) return "";

        String tmpStr = preprocess(s);
        int len = tmpStr.length();
        int[] p = new int[len];
        int C = 0, R = 0;
        int maxLen = -1;    // 最长回文子串长度
        int index = 0;      // 最长回文子串中心索引

        for (int i = 1; i < len - 1; i++) {
            p[i] = R > i ? Math.min(p[2 * C - i], R - i) : 1;

            while (tmpStr.charAt(i + p[i]) == tmpStr.charAt(i - p[i]))
                p[i]++;

            if (R < p[i] + i) {
                R = p[i] + i;
                C = i;
            }

            if (maxLen < p[i] - 1) {
                maxLen = p[i] - 1;
                index = i;
            }
        }

        int start = (index - maxLen) / 2;   // (i - p[i]) / 2
        return s.substring(start, start + maxLen);
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Manacher:
    def longest_palindrome(self, s: str) -> str:
        if s is None or len(s) == 0: return ""

        tmp_str = '^#' + ''.join([x + '#' for x in s]) + "$"
        length = len(tmp_str)
        p = [0] * length
        c, r = 0, 0
        max_len = -1
        index = 0

        for i in range(1, length - 1):
            p[i] = min(p[2 * c - i], r - i) if r > i else 1

            while tmp_str[i + p[i]] == tmp_str[i - p[i]]:
                p[i] += 1

            if r < i + p[i]:
                r = i + p[i]
                c = i

            if max_len < p[i] - 1:
                max_len = p[i] - 1
                index = i

        start = (index - max_len) // 2
        return s[start: start + max_len]
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
func preprocess(s string) string {
	result := "^#"

	for _, ch := range s {
		result += string(ch) + "#"
	}

	return result + "$"
}

func longestPalindrome(s string) string {
	if len(s) == 0 {
		return ""
	}

	tmpStr := preprocess(s)
	length := len(tmpStr)
	p := make([]int, length)
	C, R := 0, 0
	maxLen := 0
	index := 0

	for i := 1; i < length-1; i++ {
		if R > i {
			p[i] = int(math.Min(float64(p[2*C-i]), float64(R-i)))
		} else {
			p[i] = 1
		}

		for tmpStr[i+p[i]] == tmpStr[i-p[i]] {
			p[i]++
		}

		if R < i+p[i] {
			R = i + p[i]
			C = i
		}

		if maxLen < p[i]-1 {
			maxLen = p[i] - 1
			index = i
		}
	}

	start := (index - maxLen) / 2
	return s[start : start+maxLen]
}

参考资料

马拉车算法

leetcode.wang