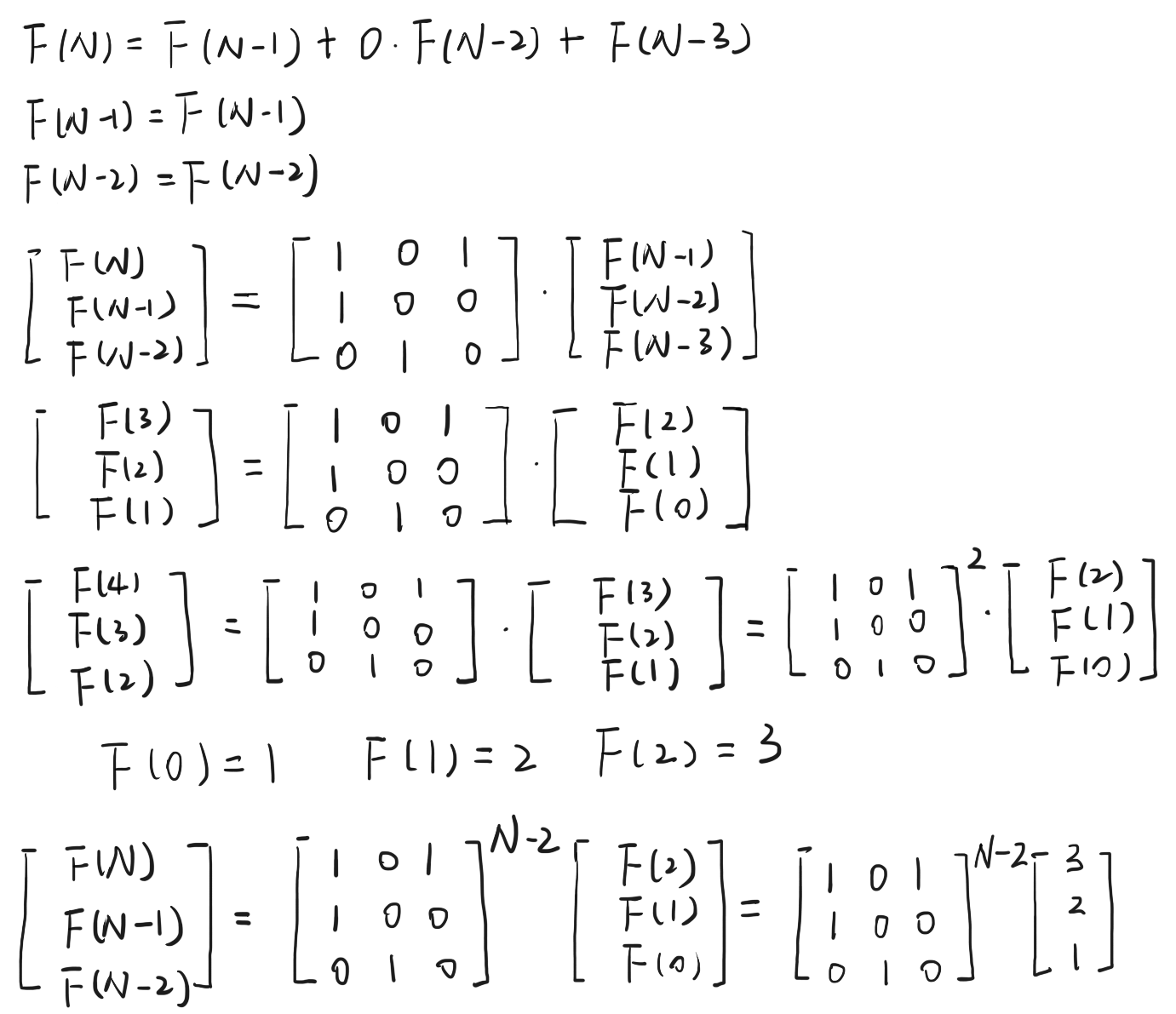题目
母牛每年生一头母牛, 新出生的母牛成长三年后也能每年生一头母牛, 假设牛不会死. 求 N 年后母牛的数量
题解
递归
归纳得 F(N) = F(N-1) + F(N-3)
该式实际上可解释为每年牛的总数等于前一年牛的总数 F(N-1) 加上三年前牛的总数 F(N-3) , 其中 F(N-3) 即为每年新增的牛的数量.
若规定牛的寿命为 10 年, 减去 F(N-10) 即可
Java
1
2
3
4
5
6
7
8
9
10
| public class CowNumber {
public static int getCowNum(int N) {
if (N <= 2) return N + 1;
return getCowNum(N - 1) + getCowNum(N - 3);
}
public static void main(String[] args) {
System.out.println(getCowNum(8));
}
}
|
Python
1
2
3
4
5
| def get_cow_number(n):
if n <= 2:
return n + 1
return get_cow_number(n - 1) + get_cow_number(n - 3)
|
Go
1
2
3
4
5
6
7
| func getCowNum(n int) int {
if n <= 2 {
return n + 1
}
return getCowNum(n-1) + getCowNum(n-3)
}
|
斐波那契数列的矩阵求法
以上算法的时间复杂度为 O(N²) 本题可参考斐波那契数列的矩阵求法, 该算法时间复杂度仅为 O(logN)
推导如下:
1
2
3
| F(n) = a*F(n-1) + b*F(n-2) + c*F(n-3)
F(n-1) = F(n-1)
F(n-2) = F(n-2)
|
本题中 a = 1, b = 0, c = 1
故可得
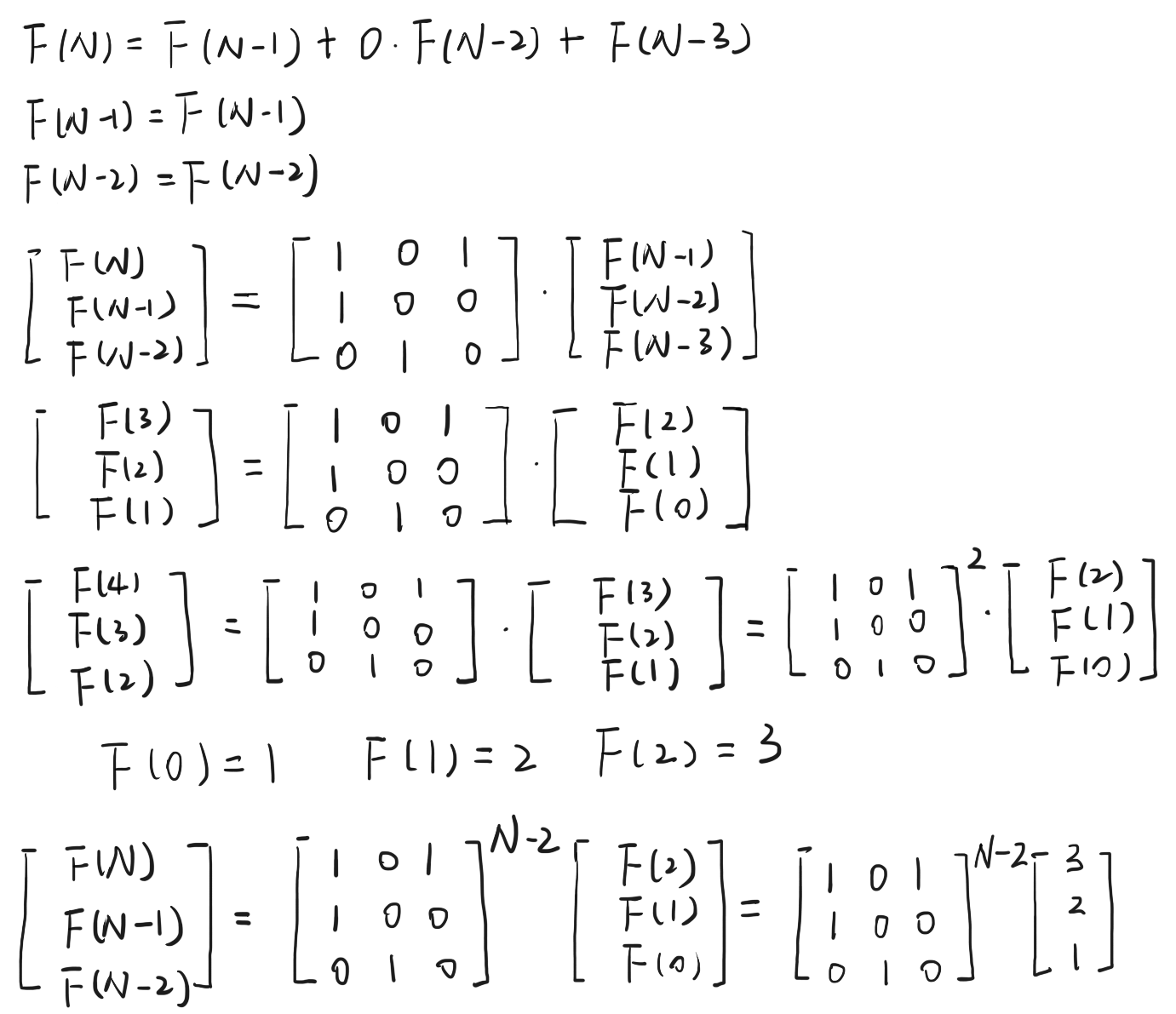
Python
1
2
3
4
5
6
7
8
9
10
11
| import numpy as np
def fib_matrix(n):
if n <= 2:
return n + 1
result = np.mat([
[1, 0, 1],
[1, 0, 0],
[0, 1, 0]
], dtype='float64') ** (n - 2) * np.mat([3, 2, 1]).T
return int(result[0, 0])
|