题目
给定一个正整数数组 arr 和一个整数 target , 如果可以任意选择 arr 中的数字, 求能否累加得到 target .
题解
暴力解法
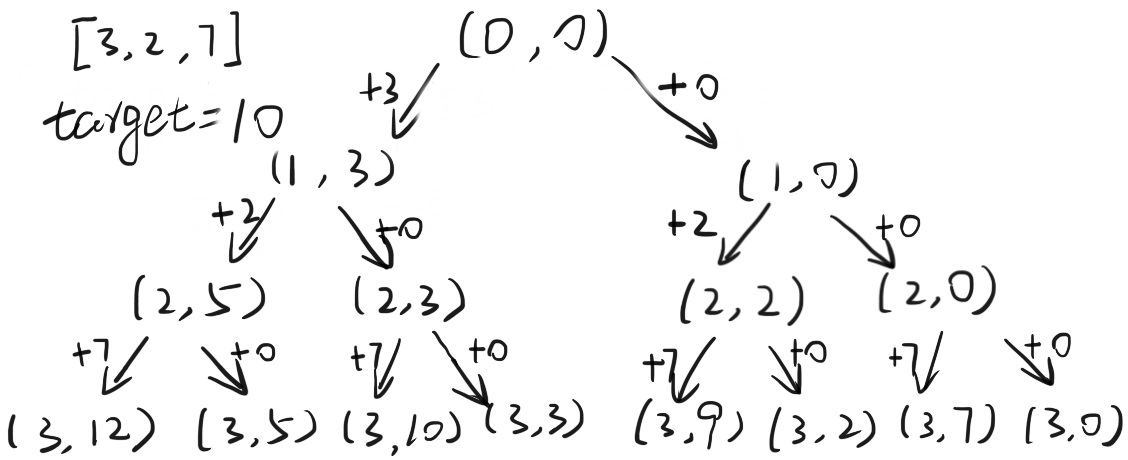
穷举所有可能的和, 判断是否含有 target , 穷举过程如下, 其中中间变量格式为 (i, sum) , i 为索引, sum 为当前的累加和, 左支表示累加 arr[i] , 右支表示跳过该值.
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class SumToTarget {
public static boolean isSum(int[] arr, int i, int sum, int target) {
if (i == arr.length)
return sum == target;
return isSum(arr, i + 1, sum + arr[i], target) || isSum(arr, i + 1, sum, target);
}
public static void main(String[] args) {
int[] arr = {3, 2, 7};
int target = 10;
System.out.println(isSum(arr, 0, 0, target));
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
| def sum_to_target(arr, i, cur_sum, target):
if i == len(arr):
return cur_sum == target
return sum_to_target(arr, i + 1, cur_sum + arr[i], target) or \
sum_to_target(arr, i + 1, cur_sum, target)
if __name__ == '__main__':
arr = [2, 3, 7]
target = 10
print(sum_to_target(arr, 0, 0, target))
|
动态规划
将暴力递归改进为动态规划时, 无需考虑原题目的含义, 只需找到迭代时各变量之间的依赖关系即可. 递归到动态规划的转化方法:
- 递归函数有
n 个参数, 就定义一个 n 维的数组
- 数组的下标是递归函数参数的取值范围
- 数组元素的值是递归函数的返回值, 这样就可以从边界值开始, 逐步填充数组,相当于计算递归函数值的逆过程。
1
| return isSum(arr, i + 1, sum + arr[i], target) || isSum(arr, i + 1, sum, target);
|
由上述代码知递归函数第 i 次递归的结果只依赖于 i+1 和 sum , 故需定义一个 i+1 和 sum 状态关系的数组. 递归函数参数 i 的取值范围为 0~arr.length , sum 的范围为全部元素都不取到全部元素的和, 以 [3, 2, 7] 为例即为 0~12 . 构成的数组如下:
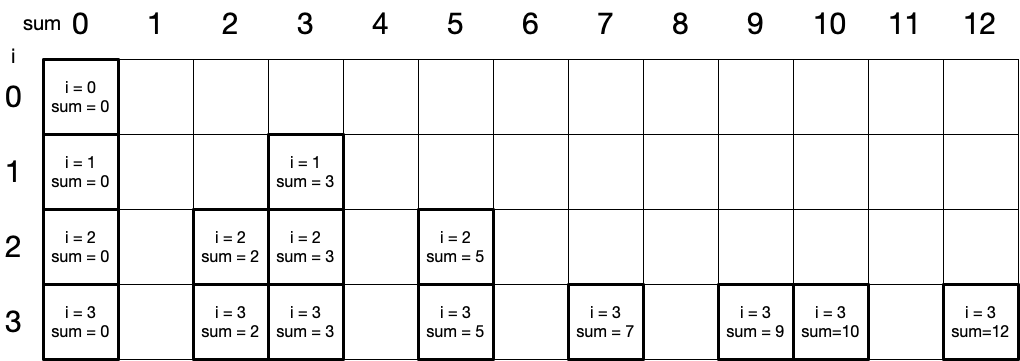
任意一格 (i, sum) 的值仅由 (i+1, sum) 和 (i+1, sum+arr[i]) 决定. 如上表所示, (1, 3) 的值取决于 (1+1, 3) 和 (1+1, 3+arr[1]) , 其中 arr[1] 为 2, 故 (1, 3) 的真值取决于 (2, 3) 和 (2, 5) 的真值.
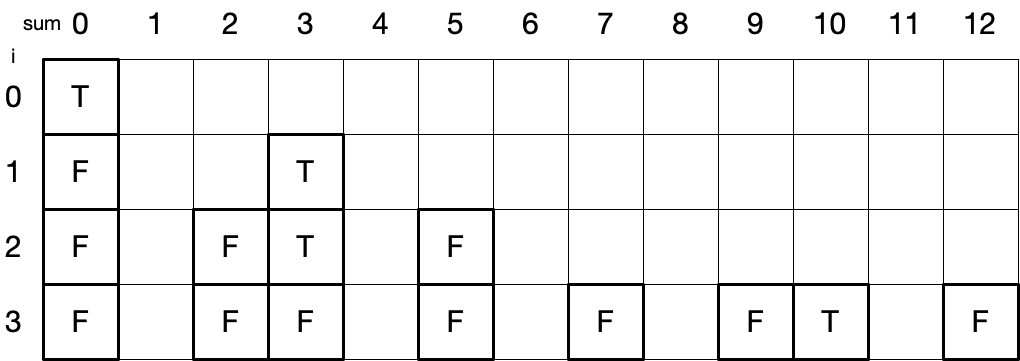
最终结果返回表中 (0, 0) 位置即可.
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class SumToTarget {
public static boolean isSum(int[] arr, int target) {
boolean[][] dp = new boolean[arr.length + 1][target + 1];
dp[i][target] = true;
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = target; j >= 0; j--) {
dp[i][j] = dp[i + 1][j];
if (j + arr[i] <= target) {
dp[i][j] = dp[i][j] || dp[i + 1][j + arr[i]];
}
}
}
return dp[0][0];
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def sum_to_target(arr, target):
row = len(arr)
dp = [[False] * (target + 1) for _ in range(row + 1)]
dp[row][target] = True
for i in range(row - 1, -1, -1):
for j in range(target, -1, -1):
if j + arr[i] <= target:
dp[i][j] = dp[i + 1][j] or dp[i + 1][j + arr[i]]
else:
dp[i][j] = dp[i + 1][j]
return dp[0][0]
|


