给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
示例:
输入:
1
2
3
4
5
| [
[1, 3, 1],
[1, 5, 1],
[4, 2, 1]
]
|
输出: 7
题解
暴力递归
从左上角到右下角, 每次移动只有向右或向下两种可能, 需递归地找出左右两个方向到右下角路径和较小者即可.
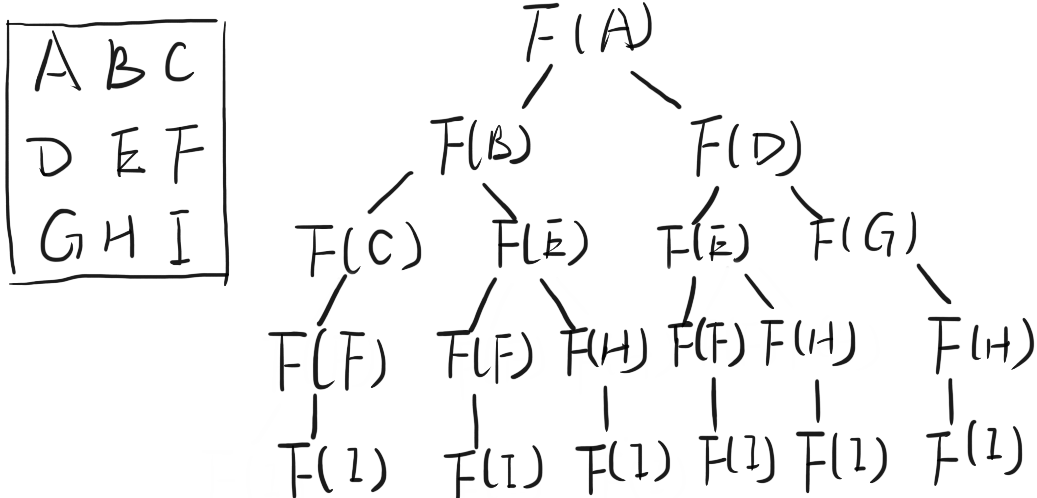
暴力递归不记录子状态的结果, F(E) , F(H), F(F) 进行了多次重复计算, 占用较多空间, 数据较多时会超时, 可改用计划搜索的方法进行优化.
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public class MinimalPathSum {
public int minPathSum(int[][] grid) {
if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
return 0;
}
return process(grid, 0, 0);
}
public static int process(int[][] grid, int i, int j) {
if (i == grid.length - 1 && j == grid[0].length - 1)
return grid[i][j];
if (i == grid.length - 1)
return grid[i][j] + process(grid, i, j + 1);
if (j == grid[0].length - 1)
return grid[i][j] + process(grid, i + 1, j);
return grid[i][j] + Math.min(process(grid, i, j + 1), process(grid, i + 1, j));
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| def get_minimal_path_sum(grid):
if not grid or len(grid) < 1 or not grid[0] or len(grid[0]) < 1:
return 0
return process(grid, 0, 0)
def process(grid, i, j):
if i == len(grid) - 1 and j == len(grid[0]) - 1:
return grid[i][j]
if i == len(grid) - 1:
return grid[i][j] + process(grid, i, j + 1)
if j == len(grid[0]) - 1:
return grid[i][j] + process(grid, i + 1, j)
return grid[i][j] + min(process(grid, i + 1, j), process(grid, i, j + 1))
|
计划搜索
将每个子状态的运算结果存入缓存中, 若之前计算过则直接返回计算结果.
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public class MinimalPathSum {
static HashMap<String, Integer> cache;
public static int minimalPathSum(int[][] grid) {
if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
return 0;
}
cache = new HashMap<>();
return process(grid, 0, 0);
}
public static int process(int[][] grid, int i, int j) {
String key = i + "_" + j;
if (cache.containsKey(key)) {
return cache.get(key);
}
int result = 0;
if (i == grid.length - 1 && j == grid[0].length - 1) {
result = grid[i][j];
} else if (i == grid.length - 1) {
result = grid[i][j] + process(grid, i, j + 1);
} else if (j == grid[0].length - 1) {
result = grid[i][j] + process(grid, i + 1, j);
} else {
result = grid[i][j] + Math.min(process(grid, i + 1, j), process(grid, i, j + 1));
}
cache.put(key, result);
return result;
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class MinimalPathSum:
def __init__(self):
self.result_dict = None
def get_minimal_path_sum(self, grid):
if not grid or len(grid) < 1 or not grid[0] or len(grid[0]) < 1:
return 0
self.result_dict = dict()
return self.process(grid, 0, 0)
def process(self, grid, i, j):
key = str(i) + "_" + str(j)
if self.result_dict.get(key):
return self.result_dict.get(key)
if i == len(grid) - 1 and j == len(grid[0]) - 1:
result = grid[i][j]
elif i == len(grid) - 1:
result = grid[i][j] + self.process(grid, i, j + 1)
elif j == len(grid[0]) - 1:
result = grid[i][j] + self.process(grid, i + 1, j)
else:
result = grid[i][j] + min(self.process(grid, i + 1, j), self.process(grid, i, j + 1))
self.result_dict[key] = result
return result
|
动态规划
左上角到右下角的最短距离与右下角到左上角最短距离相同, 为便于表示, 以下改为求右下角到左上角的最短距离.
由以上计划搜索部分知, 当矩阵中某点的位置即 i 和 j 的值确定时, 该点到左上角的最短路径就确定了, 故可单独求出矩阵中各元素到左上角的最短路径, 每个元素的最短路径值仅由其相邻的左边和上边元素决定, 其对应关系如下例, 故输出矩阵中的右下角即为左上角到右下角的最短距离.
输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| 3 8 6 0 5 9 9 6 3 4 0 5 7 3 9 3
0 9 2 5 5 4 9 1 4 6 9 5 6 7 3 2
8 2 2 3 3 3 1 6 9 1 1 6 6 2 1 9
1 3 6 9 9 5 0 3 4 9 1 0 9 6 2 7
8 6 2 2 1 3 0 0 7 2 7 5 4 8 4 8
4 1 9 5 8 9 9 2 0 2 5 1 8 7 0 9
6 2 1 7 8 1 8 5 5 7 0 2 5 7 2 1
8 1 7 6 2 8 1 2 2 6 4 0 5 4 1 3
9 2 1 7 6 1 4 3 8 6 5 5 3 9 7 3
0 6 0 2 4 3 7 6 1 3 8 6 9 0 0 8
4 3 7 2 4 3 6 4 0 3 9 5 3 6 9 3
2 1 8 8 4 5 6 5 8 7 3 7 7 5 8 3
0 7 6 6 1 2 0 3 5 0 8 0 8 7 4 3
0 4 3 4 9 0 1 9 7 7 8 6 4 6 9 5
6 5 1 9 9 2 2 7 4 2 7 2 2 3 7 2
7 1 9 6 1 2 7 0 9 6 6 4 4 5 1 0
3 4 9 2 8 3 1 2 6 9 7 0 2 4 2 0
5 1 8 8 4 6 8 5 2 4 1 6 2 2 9 7
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| 3 11 17 17 22 31 40 46 49 53 53 58 65 68 77 80
3 12 14 19 24 28 37 38 42 48 57 62 68 75 78 80
11 13 15 18 21 24 25 31 40 41 42 48 54 56 57 66
12 15 21 27 30 29 25 28 32 41 42 42 51 57 59 66
20 21 23 25 26 29 25 25 32 34 41 46 50 58 62 70
24 22 31 30 34 38 34 27 27 29 34 35 43 50 50 59
30 24 25 32 40 39 42 32 32 36 34 36 41 48 50 51
38 25 32 38 40 47 43 34 34 40 38 36 41 45 46 49
47 27 28 35 41 42 46 37 42 46 43 41 44 53 53 52
47 33 28 30 34 37 44 43 43 46 51 47 53 53 53 60
51 36 35 32 36 39 45 47 43 46 55 52 55 59 62 63
53 37 43 40 40 44 50 52 51 53 56 59 62 64 70 66
53 44 49 46 41 43 43 46 51 51 59 59 67 71 74 69
53 48 51 50 50 43 44 53 58 58 66 65 69 75 83 74
59 53 52 59 59 45 46 53 57 59 66 67 69 72 79 76
66 54 61 65 60 47 53 53 62 65 71 71 73 77 78 76
69 58 67 67 68 50 51 53 59 68 75 71 73 77 79 76
74 59 67 75 72 56 59 58 60 64 65 71 73 75 84 83
|
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public class MinimalPathSum {
public static int dynamicProgramming(int[][] grid) {
if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
return 0;
}
int row = grid.length;
int column = grid[0].length;
int[][] dp = new int[row][column];
dp[0][0] = grid[0][0];
for (int i = 1; i < row; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int j = 1; j < column; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < column; j++) {
dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
}
}
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
System.out.print(dp[i][j] + "\t");
}
System.out.println();
}
return dp[row - 1][column - 1];
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class MinimalPathSum:
def dynamic_programming(grid):
if not grid or len(grid) < 1 or not grid[0] or len(grid[0]) < 1: return 0
row = len(grid)
column = len(grid[0])
dp = [[0] * column for _ in range(row)]
dp[0][0] = grid[0][0]
for i in range(1, row):
dp[i][0] = grid[i][0] + dp[i - 1][0]
for j in range(1, column):
dp[0][j] = grid[0][j] + dp[0][j - 1]
for i in range(1, row):
for j in range(1, column):
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
return dp[row - 1][column - 1]
|
