最小生成树

最小生成树是一副连通加权无向图中一棵权值最小的生成树。一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和 (Wikipedia)。

常见算法有 Kruskal 算法和 Prim 算法

Kruskal 算法

按照边的权重顺序（从小到大）将边加入生成树中，但是若加入该边会与生成树形成环则不加入该边。直到树中含有顶点数减一条边为止。这些边组成的就是该图的最小生成树。

实现过程中, 可利用小根堆来依次返回权重最小的边, 利用并查集来避免生成树形成回路.

Java

UnionFind 定义如下

class UnionFind {
    public HashMap<GraphNode, GraphNode> parentMap;
    public HashMap<GraphNode, Integer> sizeMap;

    public UnionFind(Collection<GraphNode> nodes) {
        parentMap = new HashMap<>();
        sizeMap = new HashMap<>();

        // 初始化并查集, 此时每个结点自成一个集合, 指针指向它本身
        for (GraphNode node : nodes) {
            parentMap.put(node, node);
            sizeMap.put(node, 1);
        }
    }

    /**
     * 找到代表结点并整理结点
     *
     * @param node 当前节点
     * @return 代表结点
     */
    private GraphNode findHead(GraphNode node) {
        GraphNode parent = parentMap.get(node);
        if (parent != node) {
            parent = findHead(parent);
        }

        parentMap.put(node, parent);    // 整理结点
        return parent;
    }

    public boolean isSameSet(GraphNode node1, GraphNode node2) {
        return findHead(node1) == findHead(node2);
    }

    public void union(GraphNode a, GraphNode b) {
        if (a == null || b == null)
            return;
        GraphNode aHead = findHead(a);
        GraphNode bHead = findHead(b);

        if (aHead == bHead)
            return;

        int aSetSize = sizeMap.get(aHead);
        int bSetSize = sizeMap.get(bHead);

        if (aSetSize <= bSetSize) {
            parentMap.put(aHead, bHead);
            sizeMap.put(bHead, aSetSize + bSetSize);
        } else {
            parentMap.put(bHead, aHead);
            sizeMap.put(aHead, aSetSize + bSetSize);
        }
    }
}

Kruskal 实现

public class KruskalMST {
    public static Set<Edge> kruskalMST(Graph graph) {
        UnionFind unionFind = new UnionFind(graph.nodes.values());
        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>((a, b)->{
            return a.weight - b.weight;
        });

        priorityQueue.addAll(graph.edges);

        Set<Edge> result = new HashSet<>();
        while (!priorityQueue.isEmpty()) {
            Edge edge = priorityQueue.poll();
            if (!unionFind.isSameSet(edge.from, edge.to)) {
                result.add(edge);
                unionFind.union(edge.from, edge.to);
            }
        }

        return result;
    }
}

Python

UnionFindSet 定义见并查集

由于 Edge 对象不能够直接比较大小, 需重写 Edge 的比较函数, __lt__ 对应 < , __gt__ 对应 > , 只重写其中一个, 另一个会自动取反. 比较相等时结果相同.

class Edge:
    def __init__(self, weight, from_node, to_node):
        self.weight = weight
        self.from_node = from_node
        self.to_node = to_node

    def __lt__(self, other):
        # 重写 < 比较函数
        return True if self.weight < other.weight else False

Kruskal 实现

from heapq import *

def kruskal_mst(graph):
    union_find_set = UnionFindSet(graph.nodes.values())
    heap = []

    for edge in graph.edges:
        heappush(heap, edge)

    result = set()

    while heap:
        edge = heappop(heap)
        if not union_find_set.is_same_set(edge.from_node, edge.to_node):
            result.add(edge)
            union_find_set.union(edge.from_node, edge.to_node)

    return result

Prim 算法

从任意一个节点开始, 将与其相连的几条边全部放入一个小根堆中, 每次弹出小根堆中权重最小的边, 获取该边的另一端节点放入集合中, 并将另一端节点的所有直接相连的边放入小根堆中, 迭代直到小根堆中的边全部取出为止.

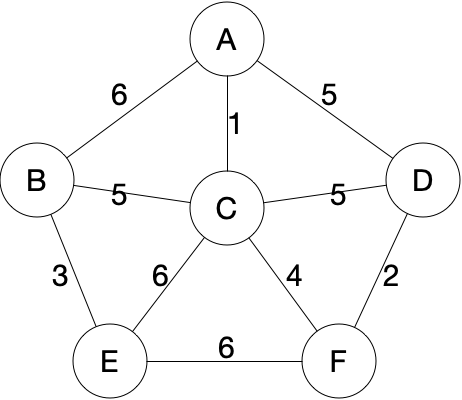
Java

public class PrimMST {
    public static Set<Edge> primMST(Graph graph) {
        PriorityQueue<Edge> priorityQueue = new PriorityQueue<>((a, b) -> {
            return a.weight - b.weight;
        });
        HashSet<GraphNode> set = new HashSet<>();
        Set<Edge> result = new HashSet<>();
		
        // 遍历所有节点, 考虑到可能有多棵生成树不相连的情况
        for (GraphNode node : graph.nodes.values()) {
            if (!set.contains(node)) {
                set.add(node);
                priorityQueue.addAll(node.edges);

                while (!priorityQueue.isEmpty()) {
                    Edge edge = priorityQueue.poll();
                    GraphNode toNode = edge.to;
                    if (!set.contains(toNode)) {
                        set.add(toNode);
                        result.add(edge);
                        priorityQueue.addAll(toNode.edges);
                    }
                }
            }
        }
        return result;
    }

    public static void main(String[] args) {
        // Prim 算法需沿着边迭代加入点, 故建立无向图时需建立双向指针
        Integer[][] nodes = {
                {6, 1, 2}, {6, 2, 1},
                {1, 1, 3}, {1, 3, 1},
                {5, 1, 4}, {5, 4, 1},
                {5, 2, 3}, {5, 3, 2},
                {3, 2, 5}, {3, 5, 2},
                {5, 3, 4}, {5, 4, 3},
                {4, 3, 6}, {4, 6, 3},
                {6, 3, 5}, {6, 5, 3},
                {2, 4, 6}, {2, 6, 4},
                {6, 5, 6}, {6, 6, 5}
        };
        Graph graph = Code_26_GraphBuilder.createGraph(nodes);
        Set<Edge> result = primMST(graph);
        for (Edge edge : result) {
            System.out.println(edge.weight);
        }
    }
}

1 3 2 4 5

Python

def prim_mst(graph):
    edge_heap = []
    node_set = set()
    result = set()

    for node in graph.nodes.values():
        if node not in node_set:
            node_set.add(node)
            for edge in node.edges:
                heappush(edge_heap, edge)

            while edge_heap:
                edge = heappop(edge_heap)
                to_node = edge.to_node
                if to_node not in node_set:
                    node_set.add(to_node)
                    result.add(edge)
                    for next_edge in to_node.edges:
                        heappush(edge_heap, next_edge)
    return result