拓扑排序算法

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，才能称为该图的一个拓扑排序（Topological sorting）：

1. 序列中包含每个顶点，且每个顶点只出现一次；
2. 若A在序列中排在B的前面，则在图中不存在从B到A的路径。

适用范围:

• 有向图
• 有入度为 0 的节点
• 图中没有环

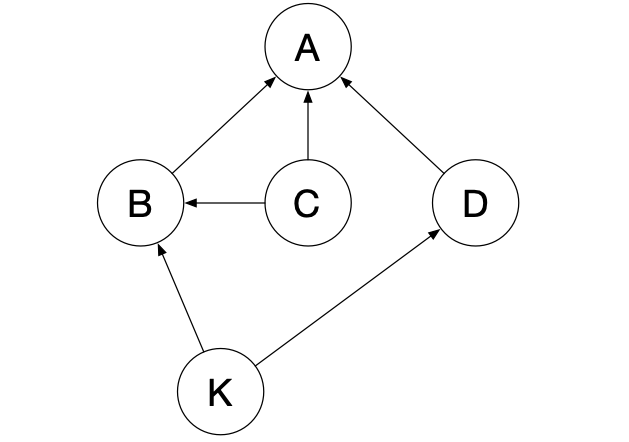
拓扑排序常应用于有依赖关系的一组事务之间的排序. 例如有依赖关系的多个模块的编译次序问题等. 假定下图中的 A , B , C , D , K 为待编译的几个模块, 箭头表示依赖关系(如 B , D 依赖于 K ), 经拓扑排序后应输出模块编译顺序, 即 K -> C -> B -> D -> A 或 C -> K -> B -> D -> A ( K 和 C , B 和 D 顺序可互换)

思路

先找到所有入度为 0 的节点并输出, 删除这些节点. 在下一次迭代中, 找到剩余节点中入度为 0 的节点并输出, 直到图中节点全部输出为止.

Java

图的结构定义及实现见另一篇博客

public class TopologySort {
    public static List<GraphNode> topologySort(Graph graph) {
        HashMap<GraphNode, Integer> inMap = new HashMap<>();
        Queue<GraphNode> zeroInQueue = new LinkedList<>();
        // 取出所有节
        for (GraphNode node : graph.nodes.values()) {
            inMap.put(node, node.in);   // 建立节点和其入度的对应关系
            if (node.in == 0)
                zeroInQueue.add(node);
        }

        List<GraphNode> result = new ArrayList<>();
        while (!zeroInQueue.isEmpty()) {
            GraphNode cur = zeroInQueue.poll();
            result.add(cur);
            // 将入度为 0 的节点的下一层节点的入度减一, 若为 0 则放入 zeroInQueue 中
            for (GraphNode next : cur.nexts) {
                inMap.put(next, inMap.get(next) - 1);
                if (inMap.get(next) == 0) {
                    zeroInQueue.add(next);
                }
            }
        }
        return result;
    }
}

Python

def topology_sort(graph):
    in_dict = dict()
    zero_in_list = []

    for node in graph.nodes.values():
        in_dict[node] = node.in_degree
        if node.in_degree == 0:
            zero_in_list.append(node)

    result = []
    while zero_in_list:
        cur = zero_in_list.pop()
        result.append(cur)

        for next in cur.nexts:
            in_dict[next] = in_dict[next] - 1
            if in_dict[next] == 0:
                zero_in_list.append(next)

    return result