Leaky Cauldron
0%

前缀树

Posted on Edited on

前缀树 又称 字典树, 是一种有序多叉树结构. 常用于做词频统计和前缀匹配. 与二叉树结构不同, 数据不保存在节点中, 而是由路径来表示. 节点中存储标记信息 (当前节点是否为某一单词的结尾、下一可能的字符等). 如下图中所示, 表示了关键字集合 {“Java”, “Rad”, “Rand”, “Rau”, “Raum”, “Rose”}。

例题 1 (LeetCode #208)

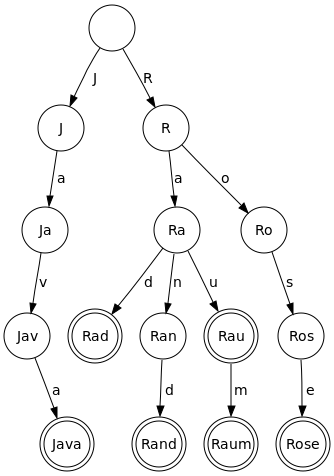
实现 Trie (前缀树)

Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

  • Trie() 初始化前缀树对象。
  • void insert(String word) 向前缀树中插入字符串 word 。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]

解释

1
2
3
4
5
6
7
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

提示：

  • 1 <= word.length, prefix.length <= 2000
  • word 和 prefix 仅由小写英文字母组成
  • insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class TrieNode {
    boolean isEnd;                           // 记录当前节点是否为某一单词的最后一个字母
    TrieNode[] children = new TrieNode[26];  // 同时记录下一个字母（索引）及其对应的节点对象
}

class Trie {
    private final TrieNode root;

    public Trie() {
        this.root = new TrieNode();
    }

    public void insert(String word) {
        TrieNode cur = root;
        for (char c : word.toCharArray()) {
            int nextIdx = c - 'a';
            if (cur.children[nextIdx] == null) {
                cur.children[nextIdx] = new TrieNode();
            }
            cur = cur.children[nextIdx];
        }
        cur.isEnd = true;
    }

    public boolean search(String word) {
        TrieNode cur = root;
        for (char c : word.toCharArray()) {
            int nextIdx = c - 'a';
            if (cur.children[nextIdx] == null) return false;
            cur = cur.children[nextIdx];
        }
        return cur.isEnd;
    }

    public boolean startsWith(String prefix) {
        TrieNode cur = root;
        for (char c : prefix.toCharArray()) {
            int nextIdx = c - 'a';
            if (cur.children[nextIdx] == null) return false;
            cur = cur.children[nextIdx];
        }
        return true;
    }
}

例题 2 (LeetCode #212)

单词搜索 II

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words， 返回所有二维网格上的单词 。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例 1：

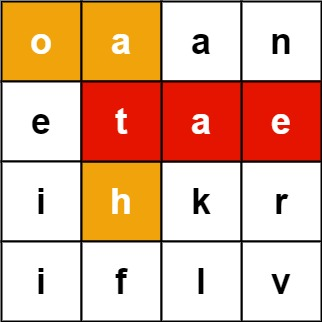
输入：board = [[“o”,”a”,”a”,”n”],[“e”,”t”,”a”,”e”],[“i”,”h”,”k”,”r”],[“i”,”f”,”l”,”v”]], words = [“oath”,”pea”,”eat”,”rain”]
输出：[“eat”,”oath”]

示例 2：

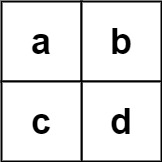
输入：board = [[“a”,”b”],[“c”,”d”]], words = [“abcb”]
输出：[]

提示：

  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 12
  • board[i][j] 是一个小写英文字母
  • 1 <= words.length <= 3 * 104
  • 1 <= words[i].length <= 10
  • words[i] 由小写英文字母组成
  • words 中的所有字符串互不相同

题解

可使用前缀树优化 words 中单词的搜索过程，以下解法中前缀树节点直接保存了以当前字母为结尾的单词，以省去添加符合条件的字符串时的二次遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class TrieNode {

    String s;
    TrieNode[] children = new TrieNode[26];

    public void insert(String s, TrieNode cur) {
        for (char c : s.toCharArray()) {
            int nextIdx = c - 'a';
            if (cur.children[nextIdx] == null) {
                cur.children[nextIdx] = new TrieNode();
            }
            cur = cur.children[nextIdx];
        }
        cur.s = s;
    }

}

class Solution {

    private Set<String> result;
    private char[][] board;
    private boolean[][] visited;
    private int m, n;
    private int[][] directions = {{0, -1}, {0, 1}, {1, 0}, {-1, 0}};

    public List<String> findWords(char[][] board, String[] words) {
        m = board.length;
        n = board[0].length;

        result = new HashSet<>();
        this.board = board;
        visited = new boolean[m][n];

        TrieNode root = new TrieNode();
        for (String word : words) root.insert(word, root);

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int cur = board[i][j] - 'a';
                if (root.children[cur] != null) dfs(i, j, root.children[cur]);
            }
        }

        return new ArrayList<>(result);
    }

    private void dfs(int i, int j, TrieNode node) {
        if (node.s != null && node.s.length() > 10) return;

        if (node.s != null) result.add(node.s);

        visited[i][j] = true;
        for (int[] direction : directions) {
            int newI = i + direction[0], newJ = j + direction[1];
            if (newI < 0 || newI >= m || newJ < 0 || newJ >= n || visited[newI][newJ]) continue;
            int nextIdx = board[newI][newJ] - 'a';
            if (node.children[nextIdx] != null) {
                dfs(newI, newJ, node.children[nextIdx]);
            }
        }
        visited[i][j] = false;
    }
}