并查集

并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

• Union：将两个子集合并成同一个集合
• isSameSet：判断两元素是否属于同一集合

并查集中的元素类似单链表中的结点, 其指针指向该节点的父结点, 集合的代表结点的指针指向它本身.

在合并两个两个集合的过程中, 一般将小的集合挂载大集合的代表结点之后. 如下图中的两个集合合并, 4 将挂在 2 下, 新集合的代表结点即为 2.

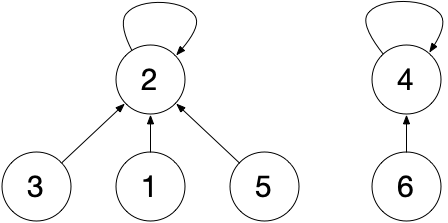
在查询 (执行 isSameSet 方法) 的过程中, 只需判断两结点所在集合的代表结点是否相同即可判断是否为同一集合.

查询或合并集合时, 若集合未经整理, 即包含多层结点 ( 如3->1->5->2 ), 需整理为如图中的仅有两层的形式, 以减少下次查询的操作数.

实现

Java

使用 HashMap 来表示结点之间的关系, (key, value) 即表示 key 的父节点是 value. 用另一个 HashMap 来存各储代表结点和集合大小, 若某结点不是代表结点, 则该节点的 size 信息无效.

class Data {
    // 自定义数据类型
}

public class UnionFindSet {
    public HashMap<Data, Data> parentMap;
    public HashMap<Data, Integer> sizeMap;

    public UnionFindSet(List<Data> nodes) {
        parentMap = new HashMap<>();
        sizeMap = new HashMap<>();

        // 初始化并查集, 此时每个结点自成一个集合, 指针指向它本身
        for (Data node : nodes) {
            parentMap.put(node, node);
            sizeMap.put(node, 1);
        }
    }

    /**
     * 找到代表结点并整理结点
     *
     * @param node 当前节点
     * @return 代表结点
     */
    private Data findHead(Data node) {
        Data parent = parentMap.get(node);
        if (parent != node) {
            parent = findHead(parent);
        }

        parentMap.put(node, parent);    // 整理结点
        return parent;
    }

    public boolean isSameSet(Data node1, Data node2) {
        return findHead(node1) == findHead(node2);
    }

    public void union(Data a, Data b) {
        if (a == null || b == null)
            return;
        Data aHead = findHead(a);
        Data bHead = findHead(b);

        if (aHead == bHead)
            return;

        int aSetSize = sizeMap.get(aHead);
        int bSetSize = sizeMap.get(bHead);

        if (aSetSize <= bSetSize) {
            parentMap.put(bHead, aHead);
            sizeMap.put(bHead, aSetSize + bSetSize);
        } else {
            parentMap.put(aHead, bHead);
            sizeMap.put(aHead, aSetSize + bSetSize);
        }
    }
}

Python

class Data:
    pass
       
class UnionFindSet:
    parent_dict = dict()
    size_dict = dict()

    def __init__(self, nodes):
        for node in nodes:
            self.parent_dict[node] = node
            self.size_dict[node] = 1

    def find_head(self, node):
        parent = self.parent_dict.get(node)
        if parent != node:
            self.find_head(parent)

        self.parent_dict[node] = parent
        return parent

    def is_same_set(self, node1, node2):
        return self.find_head(node1) == self.find_head(node2)

    def union(self, node1, node2):
        if node1 and node2:
            head1 = self.find_head(node1)
            head2 = self.find_head(node2)

            if head1 == head2:
                return

            size1 = self.size_dict.get(head1)
            size2 = self.size_dict.get(head2)

            if size1 <= size2:
                self.parent_dict[head1] = head2
                self.size_dict[head2] = size1 + size2
            else:
                self.parent_dict[head2] = head1
                self.size_dict[head1] = size1 + size2

时间复杂度

当查询次数和合并次数达到 O(N) 或以上时, 单次查询和单次合并的时间复杂度平均为 O(1)