请把纸条竖着放在桌⼦上,然后从纸条的下边向上⽅对折,压出折痕后再展 开。此时有1条折痕,突起的⽅向指向纸条的背⾯,这条折痕叫做“下”折痕 ;突起的⽅向指向纸条正⾯的折痕叫做“上”折痕。如果每次都从下边向上⽅ 对折,对折N次。请从上到下计算出所有折痕的⽅向。
给定折的次数n,请返回从上到下的折痕的数组,若为下折痕则对应元素为”down”,若为上折痕则为”up”.
测试样例:
题解
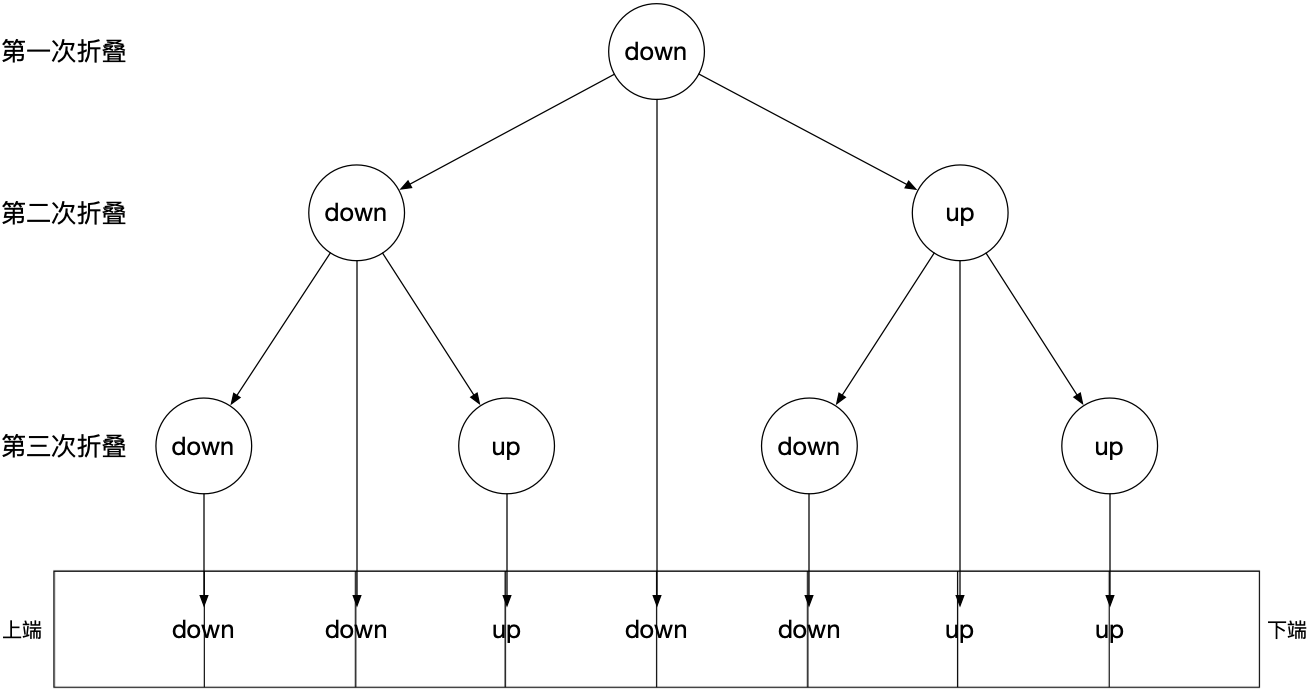
该题可看作一棵二叉树, 树的头结点为 down, 所有左子树的头结点都为 down, 所有右子树的头结点都为 up, 最终从上到下的折痕顺序为该二叉树的中序遍历结果.
因左右子树的头结点分别为 down 或 up, 故可用 down 的布尔值代替左右, 省去创建节点的空间. 以下实现最大空间复杂度为树的高度, 即折叠次数.
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public class FoldPaper {
public static void printAllFolds(int N) {
printProcess(1, N, true);
}
public static void printProcess(int i, int N, boolean down) {
if (i > N)
return;
printProcess(i + 1, N, true);
System.out.print(down ? "down " : "up ");
printProcess(i + 1, N, false);
}
}
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
| def print_all_folds(N):
print_process(1, N, True)
def print_process(i, N, down):
if i > N: return
print_process(i + 1, N, True)
print("down", end=" ") if down else print("up", end=" ")
print_process(i + 1, N, False)
print_all_folds(4)
|
