Leaky Cauldron
0%

切割金条问题

Posted on Edited on

题目

一块金条切成两半, 是需要花费和长度数值一样的铜板的. 比如长度为 20 的 金条, 不管切成长度多大的两半, 都要花费 20 个铜板. 一群人想整分整块金条, 怎么分最省铜板?

例, 给定数组 {10,20,30}, 代表一共三个人, 整块金条长度为 10 + 20 + 30 = 60 . 金条要分成 10, 20, 30 三个部分.

  • 如果先把长度 60 的金条分成 10 和 50 , 花费 60 再把长度 50 的金条分成 20 和 30, 花费 50 , 一共花费 110 铜板.
  • 如果先把长度 60 的金条分成 30 和 30, 花费 60 再把长度 30 金条分成 10 和 20 ，花费 30 一共花费 90 铜板.

输入一个数组, 返回分割的最小代价.

题解

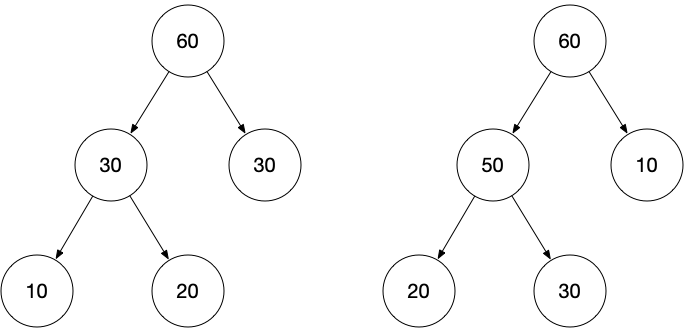
如图, 该问题可看作哈夫曼树, 树中的叶结点即为最终的划分结果, 相当于给了叶结点, 求什么情况下非叶结点的和最小. 可采用贪心算法, 利用堆结构. 将所有节点存入小根堆中. 每次依次弹出两个元素, 求和, 并将和放回小根堆中, 循环计算即可得到最小值.

Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import java.util.PriorityQueue;

public class MinimalCost {
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();

    public int getMinimalCost() {
        while (priorityQueue.size() != 1) {
            int tmp1 = priorityQueue.poll();
            int tmp2 = priorityQueue.poll();
            priorityQueue.add(tmp1 + tmp2);
        }

        return priorityQueue.peek();
    }
}
Python
1
2
3
4
5
6
7
8
9
10
11
from heapq import *

def get_minimal_cost(result_list):
    heapify(result_list)
    
    while len(result_list) != 1:
        tmp1 = heappop(result_list)
        tmp2 = heappop(result_list)
        heappush(result_list, tmp1 + tmp2)
    
    return result_list[0]